Question

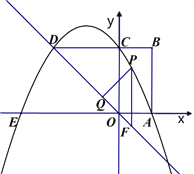
【题目】如图，在矩形OABC中，点A，点C分别在x轴和y轴上，点B（1，2）.抛物线y=ax2+bx+c经过点A、C，交BC延长线于D，与x轴另一个交点为E，且AE=4.

（1）求抛物线的表达式；

（2）点P是直线OD上方抛物线上的一个动点，PF∥y轴,PQ⊥OD，垂足为Q.

①猜想：PQ与FQ的数量关系，并证明你的猜想；

②设PQ的长为，点P的横坐标为m，求与m的函数表达式，并求的最大值；

（3）如果M是抛物线对称轴上一点，在抛物线上是否存在一点N，使得以M、N、C、E为顶点的四边形是平行四边形？若存在，直接写出N点坐标；若不存在，请说明理由.

Answer 1

【答案】（1）抛物线的表达式是y=；（2）①PQ=FQ；②l的最小值为；（3）当CE是平行四边形的边时，则有N（2，）或（-4，）；当CE是平行四边形的对角线时，则有N（-2，2）