题目内容
【题目】运用图形变化的方法研究下列问题:如图,AB是⊙O的直径,CD,EF是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8。则图中阴影部分的面积是__________.

【答案】![]() π
π
【解析】分析:作直径CG,连接OD,OE,OF,DG,则根据圆周角定理求得DG的长,证明DG=EF,则S扇形ODG=S扇形OEF,然后根据三角形的面积公式证明S△OCD=S△ACD,S△OEF=S△AEF,则S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆,即可求解.
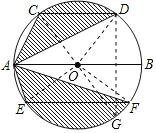
详解:作直径CG,连接OD,OE,OF,DG,
∵CG是圆的直径,
∴∠CDG=90°,则DG=![]() ,
,
又∵EF=8,
∴DG=EF,
∴弧DG=弧EF,
∴S扇形ODG=S扇形OEF,
∵AB∥CD∥EF,
∴S△OCD=S△ACD,S△OEF=S△AEF,
∴S阴影=S扇形OCD+S扇形OEF=S扇形OCD+S扇形ODG=S半圆![]() π×52=
π×52=![]() π,故答案为:
π,故答案为:![]() π.
π.
点睛:本题考查扇形面积的计算,圆周角定理,本题中找出两个阴影部分面积之间的联系是解题的关键.

练习册系列答案
相关题目