Question

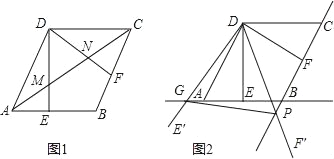
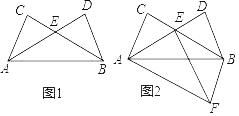
【题目】如图1，点C、D是线段AB同侧两点，且AC＝BD，∠CAB＝∠DBA，连接BC，AD交于点 E．

（1）求证：AE＝BE；

（2）如图2，△ABF与△ABD关于直线AB对称，连接EF．

①判断四边形ACBF的形状，并说明理由；

②若∠DAB＝30°，AE＝5，DE＝3，求线段EF的长．

Answer 1

【答案】(1)证明见解析；（2）①四边形ACBF为平行四边形，理由见解析；②EF=7.

【解析】

（1）利用SAS证△ABC≌△BAD可得．

（2）①根据题意知：AC=BD=BF，并由内错角相等可得AC∥BF，所以由一组对边平行且相等的四边形是平行四边形，可得结论；

②如图2，作辅助线，证明△ADF是等边三角形，得AD=AE+DE=3+5=8，根据等腰三角形三线合一得AM=DM=4，最后利用勾股定理可得FM和EF的长．

（1）证明：在△ABC和△BAD中，

∵，

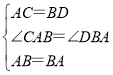∴△ABC≌△BAD（SAS），

∴∠CBA=∠DAB，

∴AE=BE；

（2）解：①四边形ACBF为平行四边形；

理由是：由对称得：△DAB≌△FAB，

∴∠ABD=∠ABF=∠CAB，BD=BF，

∴AC∥BF，

∵AC=BD=BF，

∴四边形ACBF为平行四边形；

②如图2，过F作FM⊥AD于，连接DF，

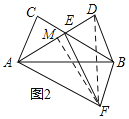
∵△DAB≌△FAB，

∴∠FAB=∠DAB=30°，AD=AF，

∴△ADF是等边三角形，

∴AD=AE+DE=3+5=8，

∵FM⊥AD，

∴AM=DM=4，

∵DE=3，

∴ME=1，

Rt△AFM中，由勾股定理得：FM===4，

∴EF==7．