题目内容
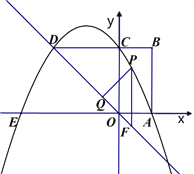
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,以点
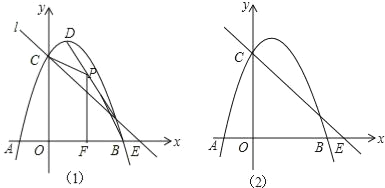
,以点![]() 为顶点的平行四边形有三个,记第四个顶点分别为
为顶点的平行四边形有三个,记第四个顶点分别为![]() ,如图所示.
,如图所示.
(1)若![]() ,则点
,则点![]() 的坐标分别是( ),( ),( );
的坐标分别是( ),( ),( );
(2)是否存在点![]() ,使得点
,使得点![]() 在同一条抛物线上?若存在,求出点
在同一条抛物线上?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
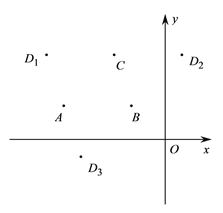
【答案】(1)![]() (-3,3),
(-3,3),![]() (1,3),
(1,3),![]() (-3,-1)(2)不存在
(-3,-1)(2)不存在
【解析】分析: (1)根据平行四边形对边相等的性质即可得到点![]() 的坐标.
的坐标.
(2)不存在. 假设满足条件的C点存在,即A,B,![]() ,
,![]() ,
,![]() 在同一条抛物线上,则线段AB的垂直平分线
在同一条抛物线上,则线段AB的垂直平分线![]() 即为这条抛物线的对称轴,而
即为这条抛物线的对称轴,而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n). 而
,即点C的坐标为(-2,n). 而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n).根据
,即点C的坐标为(-2,n).根据![]() 为抛物线的顶点.设出抛物线的方程,把点B的坐标代入得
为抛物线的顶点.设出抛物线的方程,把点B的坐标代入得![]() .把点
.把点![]() 的坐标代入得到
的坐标代入得到![]() ,与
,与![]() 矛盾. 所以不存在满足条件的C点.
矛盾. 所以不存在满足条件的C点.
(1)![]() (-3,3),
(-3,3),![]() (1,3),
(1,3),![]() (-3,-1)
(-3,-1)
(2)不存在. 理由如下:
假设满足条件的C点存在,即A,B,![]() ,
,![]() ,
,![]() 在同一条抛物线上,则线段AB的垂直平分线
在同一条抛物线上,则线段AB的垂直平分线![]() 即为这条抛物线的对称轴,而
即为这条抛物线的对称轴,而![]() ,
,![]() 在直线
在直线![]() 上,则
上,则![]()
![]() 的中点C也在抛物线对称轴上,故
的中点C也在抛物线对称轴上,故![]() ,即点C的坐标为(-2,n).
,即点C的坐标为(-2,n).
由题意得:![]() (-4,n),
(-4,n),![]() (0,n),
(0,n),![]() (-2,
(-2,![]() ).
).
注意到![]() 在抛物线的对称轴上,故
在抛物线的对称轴上,故![]() 为抛物线的顶点. 设抛物线的表达式是
为抛物线的顶点. 设抛物线的表达式是![]() .
.
当![]() 时,
时,![]() ,代入得
,代入得![]() .
.
所以![]() .
.
令![]() ,得
,得![]() ,解得
,解得![]() ,与
,与![]() 矛盾.
矛盾.
所以不存在满足条件的C点.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目