题目内容
【题目】如图,⊙C经过原点且与两坐标轴分别交于点A与点B,点A的坐标为(0,8),M是劣弧BO上任一点,∠BMO=120°,求:
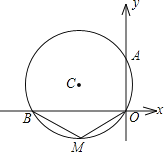
(1)⊙C的半径;
(2)圆心C的坐标.
【答案】(1)圆的半径为8;(2)点C的坐标为![]() .
.
【解析】
(1)连接AB,由于∠AOB是直角,根据圆周角定理可知AB必为⊙C的直径,即C是AB的中点,已知A点坐标,关键是求出B点的坐标.由图知:四边形ABMO是圆的内接四边形,因此内对角∠BAO、∠BMO互补,由此求得∠BAO的度数,进而可在Rt△BAO中,根据直角三角形的性质得到OB的长,从而确定点B的坐标,由此得解.
(2)作CD⊥OB于点D,利用垂径定理以及解直角三角形求得BD的长,从而求得答案,
(1)解:连接AB,过点C作CD⊥OB于点D,
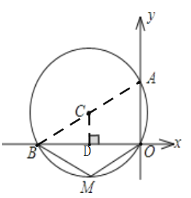
∴OD=BD,
∵∠AOB=90°
∴AB是圆O的直径,
∵四边形AOMB是圆C的内接四边形,
∴∠BAO+∠BMO=180°
∴∠BAO=180°-120°=60°
∴∠ABO=90°-60°=30°
∴AB=2OA=2×8=16,
∴圆的半径为8.
(2)解: 在Rt△CDB中,∠CBD=30°,CB=4
∴CD=8÷2=4,
BD=OD=CBcos∠CBD=![]()
∴点C的坐标为![]()

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目