Question

【题目】在平面直角坐标系中，设二次函数y＝ax2﹣4ax，其中为常数且a＜0．

（1）若函数y＝ax2﹣4ax的图象经过点（2，4），求此函数表达式；

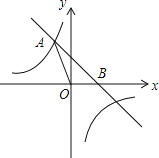
（2）若抛物线y＝ax2﹣4ax的顶点在双曲线上，试说明k的符号；

（3）已知（m，y1）、（m+1，y2）、（m+2，y3），（0＜m＜1）都是抛物线y＝ax2﹣4ax（a＜0）上的点，请判断y1，y2，y3的大小，并说明理由﹒

Answer 1

【答案】（1）此函数表达式为：y＝﹣x2+4x；（2）k＞0，见解析；（3）当0＜m＜时，2﹣m＞m+1，y3＞y2＞y1；当m＝时，y3＝y2＞y1；当＜m＜1时，m+1＞2﹣m＞m，y2＞y3＞y1；理由见解析

【解析】

（1）把点（2，4）代入y＝ax2﹣4ax中，可得a的值，由此得函数表达式；

（2）将抛物线的解析式配方后可得顶点坐标，代入反比例函数解析式，可得k的符号；

（3）根据抛物线对称轴和开口方向可得增减性，根据0＜m＜1，可确定m和m+1在对称轴的左侧，m+2在对称轴的右侧，根据对称性和增减性可得结论．

解：（1）把点（2，4）代入y＝ax2﹣4ax中得：

4a﹣8a＝4，

a＝﹣1，

∴此函数表达式为：y＝﹣x2+4x；

（2）y＝ax2﹣4ax＝a（x2﹣4x+4﹣4）＝a（x﹣2）2﹣4a，

∴顶点（2，﹣4a），

∵顶点在双曲线上，

∴k＝2×（﹣4a）＝﹣8a，

∵a＜0，

∴k＞0；

（3）∵a＜0

∴抛物线开口向下，

∵抛物线对称轴是x＝2，

∴当m＜2时，y随x的增大而增大，且x＝m+2与x＝2﹣m对称，

∵m＜m+1＜2，

∴y1＜y2，

（2﹣m）﹣（m+1）＝1﹣2m，

当0＜m＜时，2﹣m＞m+1，y3＞y2＞y1，

当m＝时，y3＝y2＞y1；

当＜m＜1时，m+1＞2﹣m＞m，y2＞y3＞y1．