题目内容
有一个二次函数的图象，三位学生分别说出了它的一些特点．
甲：对称轴是直线x=4；
乙：与x轴两交点的横坐标都是整数；
丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3；
请写出满足上述全部特点的二次函数解析式：
y=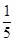
（x﹣3）（x﹣5）．
解析试题分析：由对称轴是直线x=4，与x轴两交点的横坐标都是整数，可设与x轴两交点坐标为（3，0），（5，0），又因为以函数与x轴，y轴交点为顶点的三角形面积为3，可得与y轴的交点的坐标为（0，3）．利用交点式y=a（x﹣x1）（x﹣x2），求出解析式．
试题解析：此题答案不唯一
∵对称轴是直线x=4，与x轴两交点的横坐标都是整数
可设与x轴两交点坐标为（3，0），（5，0）
又因为以函数与x轴，y轴交点为顶点的三角形面积为3
可得与y轴的交点的坐标为（0，3）
设解析式y=a（x﹣3）（x﹣5）
把点（0，3）代入得a=．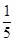
∴解析式y=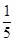（x﹣3）（x﹣5）．
考点: 待定系数法求二次函数解析式.
练习册系列答案
相关题目
上向右跳动，得到点P2、P3，这时△P1P2P3的面积为 。
的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…Cn在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形，∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An﹣1BnAn=60°，菱形An﹣1BnAnCn的周长为 ．
x+c与x轴交于点A（4，0）、B（-1，0），与y轴交于点C，连接AC，点M是线段OA上的一个动点（不与点O、A重合），过点M作MN∥AC，交OC于点N，将△OMN沿直线MN折叠，点O的对应点O′落在第一象限内，设OM=t，△O′MN与梯形AMNC重合部分面积为S．
，顶点随着t的增大向上移动时，求t的取值范围．
交于A，B两点，且A点在y轴左侧，P点的坐标为（0，﹣4），连接PA，PB．有以下说法：
时，BP2=BO•BA；
．
，点A的对应点为
，则抛物线上PA段扫过的区域（阴影部分）的面积为 .