题目内容
已知抛物线y=x2﹣4x+3.
(1)求该抛物线的顶点坐标和对称轴方程;
(2)求该抛物线与x轴的交点坐标;
(3)当x为何值时,y≤0.
(1)顶点坐标(2,-1),对称轴方程为x=2;
(2)(1,0)、(3,0);
(3)当1<x<3时,y≤0.
解析试题分析:(1)把抛物线方程转化为顶点式方程,由解析式可直接写出答案;
(2)令y=0,求得相应的x的值,即为抛物线与x轴交点的横坐标;
(3)根据图示直接写出答案.
试题解析:(1)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴该抛物线的顶点坐标是(2,﹣1),对称轴方程为x=2;
(2)令y=0,则x2﹣4x+3=0,
所以(x﹣1)(x﹣3)=0,
解得 x1="1" x2=3.
则该抛物线与x轴交点坐标是(1,0)、(3,0);
(3)由(1)、(2)知,抛物线的顶点坐标是(2,﹣1),对称轴方程为x=2,x轴交点坐标是(1,0)、(3,0).
又∵抛物线开口方程向上,与y轴交点坐标是(0,3),
∴其大致图象如图所示.
根据图示知,当1<x<3时,y≤0.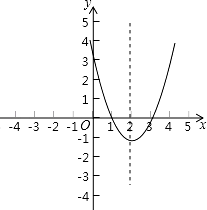
考点:1.抛物线与x轴的交点;2.二次函数的性质;3.二次函数与不等式(组).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
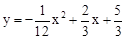 ,则铅球推出距离 米.
,则铅球推出距离 米.



 )作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.
)作直线PN⊥x轴于点N,交抛物线于点B.点B关于抛物线对称轴的对称点为C.连结CB,CP.


 .
. ﹣m(0<m<
﹣m(0<m<