题目内容
【题目】如图,O是直线AB上的一点,OC为任一射线,OD平分∠BOC,OE平分∠AOC.
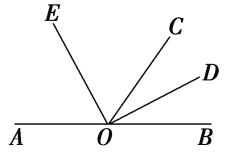
(1)指出图中∠AOD的补角和∠BOE的补角;
(2)若∠BOC=68°,求∠COD和∠EOC的度数;
(3)∠COD与∠EOC具有怎样的数量关系?
【答案】(1)∠AOD的补角为∠BOD,∠COD,∠BOE的补角为∠EOC,∠AOE;(2)∠COD=34°,∠EOC=56°;(3)∠COD与∠EOC互余.
【解析】
(1)根据互为补角的和等于180°找出即可;
(2)根据角平分线的定义求出∠COD的度数即可,先求出∠AOC的度数,再根据角平分线的定义解答;
(3)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
(1)∠AOD的补角为∠BOD,∠COD,∠BOE的补角为∠AOE,∠COE;
(2)∵OD平分∠BOC,∠BOC=68°,∴∠COD=![]() ∠BOC=
∠BOC=![]() ×68°=34°,
×68°=34°,
∵∠BOC=68°,∴∠AOC=180°﹣∠BOC=180°﹣68°=112°,
∵OE平分∠AOC,∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×112°=56°;
×112°=56°;
(3)∵OD平分∠BOC,OE平分∠AOC,∴∠COD=![]() ∠BOC,∠EOC=
∠BOC,∠EOC=![]() ∠AOC,∴∠COD+∠EOC=
∠AOC,∴∠COD+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ×180°=90°,∴∠COD与∠EOC互余.
×180°=90°,∴∠COD与∠EOC互余.

练习册系列答案
相关题目