题目内容
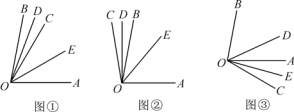
【题目】如图①,已知∠AOB=80°,OC是∠AOB内的一条射线,OD,OE分别平分∠BOC和∠COA.
(1)求∠DOE的度数;
(2)当射线OC绕点O旋转到OB的左侧时如图②(或旋转到OA的右侧时如图③),OD,OE仍是∠BOC和∠COA的平分线,此时∠DOE的大小是否和(1)中的答案相同?若相同,请选取一种情况写出你的求解过程;若不相同,请说明理由.
【答案】(1) 40°;(2) 40°.
【解析】
(1)利用角平分线定义,得出∠DOE=![]() ∠BOC+
∠BOC+![]() ∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
∠AOC,然后根据∠AOB=80°即可求出∠DOE的度数;
(2)∠DOE的大小与(1)中答案相同,仍为40°.由角平分线的定义及角的和差即可得出结论.
(1)∵OD、OE分别是∠BOC和∠COA的平分线,∴∠COD=![]() ∠BOC,∠COE=
∠BOC,∠COE=![]() ∠AOC,∴∠DOE=∠COD+∠COE=
∠AOC,∴∠DOE=∠COD+∠COE=![]() ∠BOC+
∠BOC+![]() ∠AOC=
∠AOC=![]() ∠AOB=40°;
∠AOB=40°;
(2)∠DOE的大小与(1)中答案相同,仍为40°.选图②说明:∠DOE=∠COE-∠COD=![]() ∠AOC-
∠AOC-![]() ∠BOC=
∠BOC=![]() (∠AOC-∠BOC)=
(∠AOC-∠BOC)=![]() ∠AOB=
∠AOB=![]() ×80°=40°.
×80°=40°.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
【题目】观察下列三行数:
2 | 6 | 18 | 54 | 162…① |
-1 | 3 | 15 | 51 | 159…② |
-1 | -3 | -9 | -27 | -81…③ |
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数有什么关系?
(3)每行取第6个数计算它们的和.