题目内容
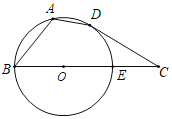
【题目】如图，四边形ABCD的三个顶点A、B、D在⊙O上，BC经过圆心O，且交⊙O于点E，∠A＝120°，∠C＝30°．
（1）求证：CD是⊙O的切线．
（2）若CD＝6，求BC的长．
（3）若⊙O的半径为4，则四边形ABCD的最大面积为 ．
【答案】（1）证明见解析；（2）
；（3）
．
【解析】
（1）连接
、
，根据圆内接四边形的性质得到
，求得
，又点
在
上，于是得到结论；
（2）由（1）知：
又
，设为
，则
为
，根据勾股定理即可得到结论；
（3）连接BD，OA，根据已知条件推出当四边形ABOD的面积最大时，四边形ABCD的面积最大，当OA⊥BD时，四边形ABOD的面积最大，根据三角形和菱形的面积公式即可得到结论．
解：（1）证明：连接、，
四边形
为圆内接四边形，
，
，
，又点在上，
是的切线；
（2）由（1）知：又，
，
设为，则为，
在
中，
，
即
，
，
又
，
，
；
（3）连接
，
，
，
，
，
，
，
，
，
，
，
当四边形
的面积最大时，四边形
的面积最大，
当
时，四边形的面积最大，
四边形的最大面积
，
故答案为：．
练习册系列答案
阅读快车系列答案
相关题目
