题目内容
【题目】如图,在等腰![]() 中,
中,![]() .点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.
.点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.

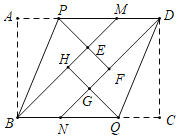
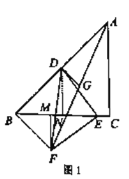
(1)如图1,若![]() ,点E与点C重合,AF与DC相交于点O.求证:
,点E与点C重合,AF与DC相交于点O.求证:![]() .
.
(2)已知点G为AF的中点.
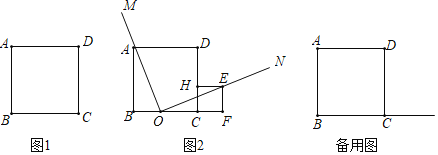
①如图2,若![]() ,求DG的长.
,求DG的长.
②若![]() ,是否存在点E,使得
,是否存在点E,使得![]() 是直角三角形?若存在,求CE的长;若不存在,试说明理由.
是直角三角形?若存在,求CE的长;若不存在,试说明理由.
【答案】(1)见解析;(2)①![]() ,②存在,CE的长为:
,②存在,CE的长为:![]() ,2或
,2或![]() ,
,![]() .
.
【解析】
(1)先证明CD=BD=AD,再证明![]() ,根据全等三角形的性质可得
,根据全等三角形的性质可得![]() ,由此即可证得结论;(2)①分别过点D,F作
,由此即可证得结论;(2)①分别过点D,F作![]() 与点N,
与点N,![]() 与点M,连接BF,先求得BF的长,再证明DG是△ABF的中位线,根据三角形的中位线定理即可求得DG的长;②分∠DEG=90°和∠EDG=90°两种情况求解即可.
与点M,连接BF,先求得BF的长,再证明DG是△ABF的中位线,根据三角形的中位线定理即可求得DG的长;②分∠DEG=90°和∠EDG=90°两种情况求解即可.
解:(1)由旋转性质得:![]() ,
,![]()
![]() 是等腰三角形,
是等腰三角形,![]()
![]() ,
,![]()
![]()
在![]() 和
和![]() 中,
中,
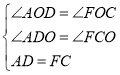
![]()
![]()
![]()
(2)①如图1,分别过点D,F作![]() 与点N,
与点N,![]() 与点M,连接BF,
与点M,连接BF,
![]()
又![]() ,
,![]()
![]() ,
,![]()
又![]() ,
,![]() ,
,![]()
![]() ,
,![]()
![]()
![]() 点D,G分别是AB,AF的中点,
点D,G分别是AB,AF的中点,
![]()
②过点D作![]() 与点H
与点H
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,有如图2,3两种情况,设
时,有如图2,3两种情况,设![]() ,
,

![]() ,
,![]() ,
,
![]() 点E在线段AF上,
点E在线段AF上,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() 或
或![]() ,
,
当![]() 时,如图4,
时,如图4,
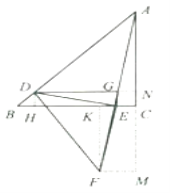
图4
过点F作![]() 与点K,延长DG交AC于点N,延长AC并截取
与点K,延长DG交AC于点N,延长AC并截取![]() ,连接FM,
,连接FM,
则![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() 四边形GECN是平行四边形,
四边形GECN是平行四边形,
∵![]() ,
,
![]() 四边形GECN是矩形,
四边形GECN是矩形,![]()
![]() 当
当![]() 时,有
时,有![]()
当![]() 时,如图5,
时,如图5,
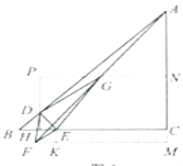
图5
过点G,F分别作AC的垂线,交射线AC于点N,M,过点E作![]() 于点K,过点D作GN的垂线,交NG的延长线于点P,则
于点K,过点D作GN的垂线,交NG的延长线于点P,则![]()
设![]() ,则
,则![]() ,
,
![]()
由![]() 可得:
可得:![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
由![]() 可得:
可得:![]()
即![]()
解得![]() ,
,![]() (舍去)
(舍去)
![]()
所以,CE的长为:![]() ,2或
,2或![]() ,
,![]()

【题目】一茶叶专卖店经销某种品牌的茶叶,该茶叶的成本价是80元/kg,销售单价不低于120元/kg.且不高于180元/kg,经销一段时间后得到如下数据:
销售单价x(元/kg) | 120 | 130 | … | 180 |
每天销量y(kg) | 100 | 95 | … | 70 |
设y与x的关系是我们所学过的某一种函数关系.
(1)直接写出y与x的函数关系式,并指出自变量x的取值范围;
(2)当销售单价为多少时,销售利润最大?最大利润是多少?
【题目】某宾馆有若干间标准房,当标准房的价格为200元时,每天入住的房间数为60间,经市场调查表明,该宾馆每间标准房的价格在170~240元之间(含170元,240元)浮动时,每天入住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| … | 190 | 200 | 210 | 220 | … |
| … | 65 | 60 | 55 | 50 | … |

(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)求![]() 关于
关于![]() 的函数表达式、并写出自变量
的函数表达式、并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为![]() (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?
(元).若不考虑其他因素,问宾馆标准房的价格定为多少元时.客房的日营业额最大?最大为多少元?