题目内容
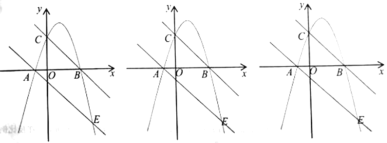
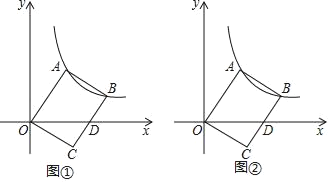
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
【答案】(1)![]() ;(2)OA=8.
;(2)OA=8.
【解析】
(1)过点A作AE⊥x轴于点E,利用三角形的面积公式结合△OAD的面积为10,可求出AE的长度,由OA,AE的长利用勾股定理可求出OE的长度,进而可得出点A的坐标,由点A的坐标,再利用待定系数法即可求出反比例函数的解析式;(2)连接AD,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,由平行线的性质可得出∠BDF=∠AOD,结合点D恰好是BC的中点可得出AE=![]() OA,OE=
OA,OE=![]() OA,BF=
OA,BF=![]() OA,DF=
OA,DF=![]() OA,S△OAD=S△OAB=2S△OBD=12
OA,S△OAD=S△OAB=2S△OBD=12![]() .由点A,B在反比例函数图象上结合反比例函数图象上点的坐标特征,可得出OF=OA,进而可得出OD=
.由点A,B在反比例函数图象上结合反比例函数图象上点的坐标特征,可得出OF=OA,进而可得出OD=![]() OA,再利用三角形的面积公式结合S△OAD=12
OA,再利用三角形的面积公式结合S△OAD=12![]() ,可求出OA的长度.
,可求出OA的长度.
(1)在图①中,过点A作AE⊥x轴于点E.
∵S△OAD=![]() ODAE=10,OD=5,
ODAE=10,OD=5,
∴![]() ×5AE=10,
×5AE=10,
∴AE=4,
∴OE=![]() =3,
=3,
∴点A的坐标为(3,4).
将A(3,4)代入y=![]() ,得:4=
,得:4=![]() ,
,
解得:k=12,
∴反比例函数的解析式为y=![]() .
.
(2)在图②中,连接AD,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
∵OA∥BC,
∴∠BDF=∠AOD=60°.
∵点D恰好是BC的中点,
∴AE=![]() OA,OE=
OA,OE=![]() OA,BF=
OA,BF=![]() OA,DF=
OA,DF=![]() OA,S△OAD=S△OAB=2S△OBD=12
OA,S△OAD=S△OAB=2S△OBD=12![]() .
.
∵反比例函数![]() 经过点A和点B,
经过点A和点B,
∴OEAE=OFBF,
∴OF=2OE=OA,
∴OD=OF﹣DF=![]() OA.
OA.
∴S△OAD=![]() ODAE=
ODAE=![]() OA2=12
OA2=12![]() ,
,
∴OA=8.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1