题目内容
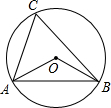如图，△ABC的顶点A、B、C均在⊙O上，∠OAC=40°，∠OBC=15°则∠AOB的度数是
- A.55°
- B.110°
- C.120°
- D.150°
B
分析：连接OC，首先根据等腰三角形的性质求出∠ACB的度数，再根据圆周角定理求解．
解答：连接OC
∵OA=OC，∠OAC=40°，
∴∠OCA=∠OAC=40°．
同理：∠OCB=15°，
∴∠ACB=55°，
∴∠A0B=2∠ACB=110°．
故选B．
点评：本题考查了圆周角定理、等腰三角形的性质以及三角形的外角和不相邻的两个内角之间的关系．
分析：连接OC，首先根据等腰三角形的性质求出∠ACB的度数，再根据圆周角定理求解．
解答：连接OC
∵OA=OC，∠OAC=40°，
∴∠OCA=∠OAC=40°．
同理：∠OCB=15°，
∴∠ACB=55°，
∴∠A0B=2∠ACB=110°．
故选B．
点评：本题考查了圆周角定理、等腰三角形的性质以及三角形的外角和不相邻的两个内角之间的关系．
练习册系列答案
备战中考寒假系列答案
相关题目
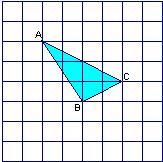
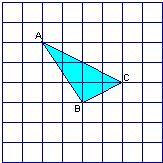
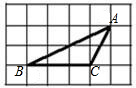如图，△ABC的顶点都是正方形网格中的格点，则sin∠ABC等于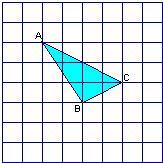
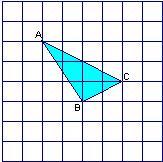
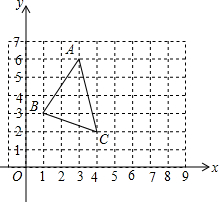如图，△ABC的顶点坐标分别为A （ 3，6 ），B （ 1，3 ），C （ 4，2 ）．如果将△ABC绕C点顺时针旋转90°，得到△A′B′C′，那么点A的对应点A′的坐标为
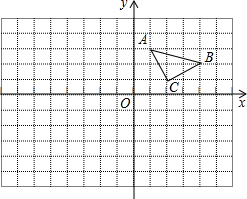如图，△ABC的顶点坐标分别为A（1，3）、B（4，2）、C（2，1）．
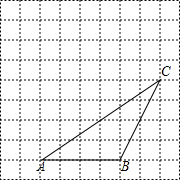如图，△ABC的顶点都在方格纸的格点上，将△ABC向左平移2格，再向上平移2格，其中每个格子的边长为1个单位长度．