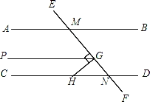
题目内容
【题目】如图①,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
(2)如图②,点G在BE上,且∠BDG=∠C.求证:△DEG∽△ECF;
(3)在(2)的条件下,已知EF=2,CE=3,求GE的长.
【答案】
(1)证明:∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEB=∠C,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,又∠DEB=∠C,
∴△DEG∽△ECF;
(3)解:∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴ ![]() ,即BD2=BEBG,
,即BD2=BEBG,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM,
又∵DM=AD,AD=BD,
∴EF=BD=2,
∵BE=CE,EF=2,CE=3,
∴22=3BG,
∴BG= ![]() ,
,
∴GE=3﹣ ![]() =
= ![]() .
.
【解析】(1)(1)根据DM∥EF得到∠AMD=∠AFE,等量代换得到∠AMD=∠A,根据等角对等边证明即可。
(2)根据三角形中位线定理得到DE∥AC,证得∠BDE=∠AFE,再根据∠BDG+∠GDE=∠C+∠FEC,证明∠GDE=∠FEC,根据相似三角形的判定定理证明。
(3)根据已知易证△BDG∽△BED,得到BD2=BEBG,再证明四边形DEFM是平行四边形,从而求出BD、BE的长,即可求得BG的长,继而得出GE的长。
【考点精析】本题主要考查了平行线的性质和三角形中位线定理的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

【题目】已知抛物线 ![]()
(1)该抛物线的对称轴是 , 顶点坐标;
(2)选取适当的数据填入下表,并在直角坐标系内描点画出该抛物线的图象;
x | … | … | |||||
y | … | … |

(3)若该抛物线上两点A(x1 , y1),B(x2 , y2)的横坐标满足x1>x2>1,试比较y1与y2的大小.