Question

【题目】（探究活动）

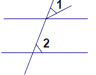
（1）问题发现：如图①，直线AB∥CD，E是AB与AD之间的一点，连接BE，CE，可以发现∠B+∠C=∠BEC．

请把下面的证明过程补充完整：

证明：过点E作EF∥AB，

∵AB∥DC（已知），EF∥AB（辅助线的作法），

∴EF∥DC（　 　）

∴∠C=∠CEF．（　 　）

∵EF∥AB，∴∠B=∠BEF（同理），

∴∠B+∠C=　 　（等量代换）

即∠B+∠C=∠BEC．

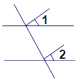
（2）拓展探究：如果点E运动到图②所示的位置，其他条件不变，试探究∠B、∠C、∠BEC的数量关系并证明；

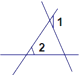
（3）解决问题：如图③，AB∥DC，∠C=120°，∠AEC=80°，则∠A=　 　．（直接写出结论，不用写计算过程）

Answer 1

【答案】（1）平行与同一条直线的两条直线互相平行；两直线平行，内错角相等；∠BEF+∠CEF；（2）∠B+∠BEC+∠C=360°，理由见解析；（3）20°

【解析】

（1）过点E作EF∥AB，根据平行线的判定得出AB∥CD∥EF，根据平行线的性质得出即可；

（2）过点E作EF∥AB，根据平行线的判定得出AB∥CD∥EF，根据平行线的性质得出即可；

（3）过点E作EF∥AB，根据平行线的判定得出AB∥CD∥EF，根据平行线的性质得出即可．

（1）过点E作EF∥AB，

∵AB∥DC（已知），

∴EF∥DC（平行与同一条直线的两条直线互相平行）

∴∠C=∠CEF．（两直线平行，内错角相等）

∵EF∥AB，

∴∠B=∠BEF（同理），

∴∠B+∠C=∠BEF+∠CEF（等量代换）

即∠B+∠C=∠BEC．

故答案为：平行与同一条直线的两条直线互相平行；两直线平行，内错角相等；∠BEF+∠CEF；

（2）∠B、∠C、∠BEC的数量关系是：∠B+∠BEC+∠C=360°

证明：过点E作EF∥AB，

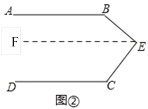
∵AB∥DC,EF∥AB，

∴EF∥DC，

∴∠B+∠BEF=180°，∠C+∠CEF=180°,

又∵∠BEC=∠BEF+∠CEF

∴∠B+∠C+∠BEC

=∠B+∠C+∠BEF+∠CEF=360°，

即：∠B+∠BEC+∠C=360°

（3） 如图③，过点E作EF∥AB，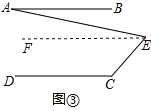

∵AB∥DC（已知），EF∥AB（辅助线的作法），
∴EF∥DC（平行于同一直线的两直线平行），
∴∠C+∠CEF=180°，∠A=∠AEF，

∴∠CEF =180°－∠C =60°

∴∠AEF =∠AEC－∠CEF=20°，
∴∠A=20°

故答案为：20°.