题目内容
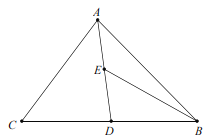
【题目】如图,在△ABC中,∠ABC=90°,BC=6,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
(1)求BH的长;
(2)若AB=12,试判断∠CBD与∠A的数量关系,请说明理由.
【答案】
(1)解:∵DH∥AB,
∴△ABC∽△DHC,
∴ ![]() ,
,
∵BC=6,AC=3CD,
∴CH=2,
∴BH=BC+CH=6+2=8;
(2)解:∠CBD=∠A,
理由是:∵AC=3CD,△ABC∽△DHC,
∴ ![]() =3,
=3,
∵AB=12,
∴DH=4,
∵DH∥AB,∠ABC=90°,
∴∠ABC=∠H=90°,
∵AB=12,BC=6,BH=8,DH=4,
∴tan∠CND= ![]() ,tanA=
,tanA= ![]() ,
,
∴∠CBD=∠A.
【解析】(1)由已知条件DH∥AB,得出△ABC∽△DHC,再得对应边成比列,建立方程,即可求出BH的长。
(2)先由△ABC∽△DHC,得出对应边成比例,求出AB的长,再证明∠H=90°,然后利用三角函数的定义分别求出tan∠CND,tanA的值,即可得出∠CBD与∠A的数量关系。
【考点精析】本题主要考查了平行线的性质和相似三角形的判定的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目