题目内容
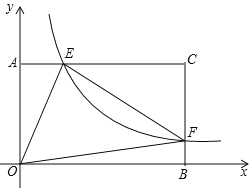
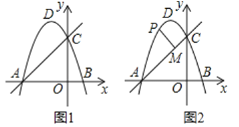
【题目】如图1,在平面直角坐标系中,抛物线y=![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)点P为线段BC上方抛物线上(不与B、C重合)的一动点,连接PC、PB,当△PBC面积最大时,在y轴找点D,使得PD﹣![]() OD的值最小时,求这个最小值.
OD的值最小时,求这个最小值.
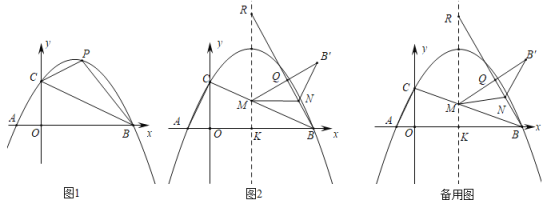
(2)如图2,抛物线对称轴与x轴交于点K,与线段BC交于点M,在对称轴上取一点R,使得KR=12(点R在第一象限),连接BR.已知点N为线段BR上一动点,连接MN,将△BMN沿MN翻折到△B'MN.当△B'MN与△BMR重叠部分(如图中的△MNQ)为直角三角形时,直接写出此时点B'的坐标.
【答案】(1)PD﹣![]() OD的值最小
OD的值最小![]() ;(2)B'(2
;(2)B'(2![]() ,12)或B'(
,12)或B'(![]() ,4)时,△MNQ为直角三角形.
,4)时,△MNQ为直角三角形.
【解析】
(1)由已知可求![]() ,
,![]() ,
,![]() ,求出直线BC的解析式,进而设点P的坐标,再根据
,求出直线BC的解析式,进而设点P的坐标,再根据![]() 面积最大时确定P点的坐标,最后根据最短路径的知识求出
面积最大时确定P点的坐标,最后根据最短路径的知识求出![]() 的最小值;
的最小值;
(2)根据题意,重叠部分可以分两种情况进行讨论,即①当MN⊥B'M,②当MN⊥BR时,![]() 为直角三角形,进而求出B'的坐标即可.
为直角三角形,进而求出B'的坐标即可.
(1)由已知可求![]() ,
,![]() ,
,![]() ,
,
∴直线BC的解析式为![]() ,直线AC的解析式为
,直线AC的解析式为![]() ,
,
设点![]() ,
,
∵过点P与直线BC垂直的直线解析式为![]() ,
,
∴设直线![]() 与直线
与直线![]() 的交点Q的坐标为
的交点Q的坐标为
![]() ,
,
∴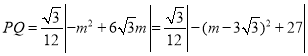 ,
,
当m=![]() 时,PQ有最大,此时
时,PQ有最大,此时![]() 面积最大,
面积最大,
∴![]() ,
,
如下图,作P点关于y轴的对称点![]() ,作直线
,作直线![]() ,
,
过点P'作直线![]() 的垂线交y轴于点D,交直线
的垂线交y轴于点D,交直线![]() 于点M,
于点M,
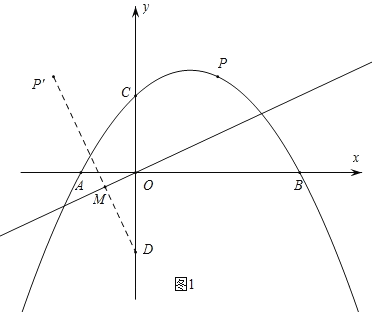
∵PD=P'D,∠DOM=60°,
∴MD=![]() OD,
OD,
∴![]() ,
,
∴![]() OD的最小值为P'M;
OD的最小值为P'M;
∵P'D的解析式为y=![]() ,
,
∴![]() ,
,
∴P'M=![]() ,
,
∴![]() 的值最小
的值最小![]() ;
;
(2)①当MN⊥B'M时,![]() 为直角三角形,
为直角三角形,
对称轴![]() ,
,
∴![]() ,
,![]() ,
,
∴KB=![]() ,
,
直线BC的解析式为![]() ,
,
∴![]() ,
,
∴MK=4,MB=8,
∴RM=8,
∴MR=KB,
∵![]() ,
,
∴∠KRB=30°,
∴∠B'=30°,
∴QM=4,B'Q=![]() ,
,
∴RQ=4,
∴QN=![]() ,
,
∴![]() ;
;
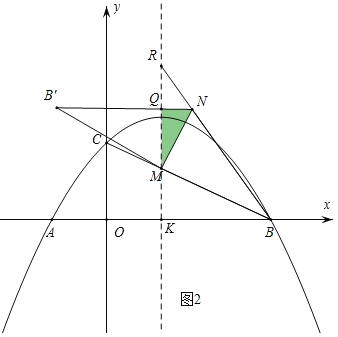
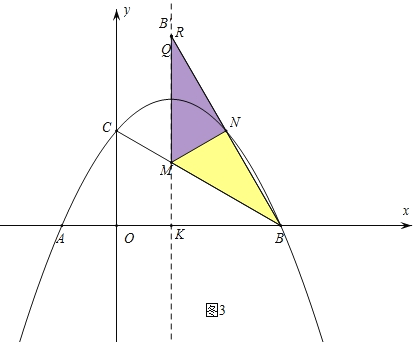
②当MN⊥BR时,![]() 为直角三角形,
为直角三角形,
∵∠MBN=∠MB'N=30°,∠KRB=30°,
∴B'与R重合,
∴![]() ;
;
综上所述:![]() 或
或![]() 时,
时,![]() 为直角三角形.
为直角三角形.

【题目】在新的教学改革的推动下,某中学初年级积极推进英语小班教学.为了了解一段时间以来的英语小班教学的学习效果,年级组织了多次定时测试,现随机选取甲,乙两个班,从中各抽取20名同学在某一次定时测试中的英语成绩,过程如下,请补充完整
收集数据:
甲班的20名同学的英语成绩统计(单位:分)
86 90 60 76 92 83 56 76 85 70
96 96 90 68 78 80 68 96 85 81
乙班的20名同学的英语成绩统计(满分为100分)(单位:分)
78 96 75 76 82 87 60 54 87 72
100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
数量分数/ 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据:
请回答下列问题:
(1)完成下表:
平均分 | 中位数 | 众数 | |
甲班 | 80.6 | 83 | a= |
乙班 | 80.35 | b= | 78 |
甲班成绩得分扇形图(x表示分数)
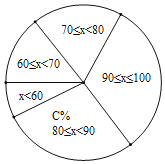
(2)在班成绩行分的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数 ,c= .
(3)根据以上数据,你认为 班(填“甲”或“乙”)的同学的学习效果更好一些,你的理由是: ;
(4)若英语定时成绩不低于80分为优秀,请估计全年级1600人中优秀人数为多少?