题目内容
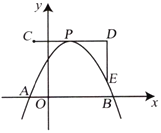
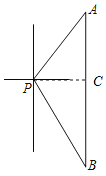
【题目】如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处.
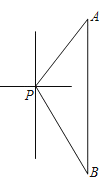
(1)若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,是否有触礁危险?
(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B处,并说明理由.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45)
≈2.45)
【答案】(1)没有触礁危险;(2)海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处,理由见解析
【解析】
(1)作PC⊥AB于C,则∠PCA=∠PCB=90°,由题意得:PA=80,∠APC=45°,∠BPC=60°,得出△APC是等腰直角三角形,∠B=30°,求出![]() ,即可得出结论;
,即可得出结论;
(2)由直角三角形的性质得出![]() ,得出
,得出![]() ,求出海轮以每小时30海里的速度从A处到B处所用的时间,即可得出结论.
,求出海轮以每小时30海里的速度从A处到B处所用的时间,即可得出结论.
解:(1)作PC⊥AB于C,如图所示:
则∠PCA=∠PCB=90°,
由题意得:PA=80,∠APC=45°,∠BPC=90°﹣30°=60°,
∴△APC是等腰直角三角形,∠B=30°,
∴![]() (海里)>50(海里),
(海里)>50(海里),
∴若灯塔P周围50海里范围内有暗礁,海轮从A处到B处的途中,没有触礁危险;
(2)海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处,理由如下:
∵∠PCB=90°,∠B=30°,
∴![]() ,
,
∴![]() ,
,
∴海轮以每小时30海里的速度从A处到B处所用的时间为:![]() (小时)>5小时,
(小时)>5小时,
∴海轮以每小时30海里的速度从A处到B处,海轮不能在5小时内到达B处.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目