Question

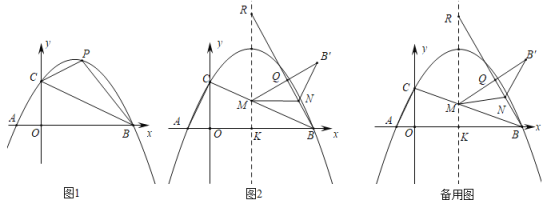
【题目】如图1，抛物线y＝﹣x2+bx+c经过点A，B，C，已知点A和C的坐标分别是（﹣4，0）和（0，4），点P在抛物线y＝﹣x2+bx+c上．

（1）求抛物线的解析式及顶点D的坐标；

（2）如图2，当点P在线段AC的上方，点P的横坐标记为t，过点P作PM⊥AC于点M，当PM＝时，求点P的坐标；

（3）若点E是抛物线对称轴上与点D不重合的一点，F是平面内的一点，当四边形CPEF是正方形时，求点P的坐标．

Answer 1

【答案】（1）y＝﹣x2﹣3x+4，(﹣，)；（2）(﹣2，16﹣7)；（3）点P坐标为(，)

【解析】

（1）根据题意直接将A、C点坐标代入二次函数表达，即可求解；

（2）由题意求出PE＝＝PM＝2，即可求解；

（3）根据题意分当CE为正方形一条边、CE为正方形的对角线两种情况，求解即可．

解：（1）将A、C点坐标代入二次函数表达式得：，解得：，

故抛物线的表达式为：y＝﹣x2﹣3x+4，

则点D的坐标为（﹣，）；

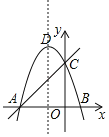
（2）设：直线AC的表达式为：y＝kx+4，

将点A坐标代入上式得：0＝﹣4k+4，解得：k＝1，

则直线AC的表达式为：y＝x+4，

过点P作y轴的平行线，交AC于点EM，

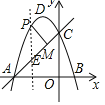
∵OA＝OC，∴∠CAB＝45°，则∠EPM＝45°，

∴PE＝＝PM＝2，

设：点P坐标为（x，﹣x2﹣3x+4），则点E坐标为（x，x+4），

PE＝﹣x2﹣3x+4﹣x﹣4＝﹣x2﹣4x＝2，

解得：x＝﹣2±（舍去﹣2﹣），

则点P的坐标为（﹣2，16﹣7）；

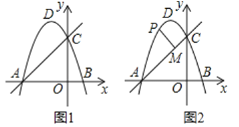
（3）当点P′在对称轴左侧时（左侧图），

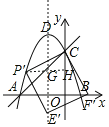
同①所证，设CH＝a，则点P′坐标为（﹣a﹣，4﹣a），

将点P′坐标代入二次函数表达式并解得：a＝（负值已舍去），

点P′的坐标为（，），

同理当点P′′在对称轴右侧时（右侧图），

点P″的坐标为（﹣1，）或（，）．

备注：本题如果是这样表述：当四边形C，P，E，F是正方形时，求点P的坐标．

则需要考虑：CE为正方形一条边时，

过点E作EG⊥y轴，交y轴于点G，

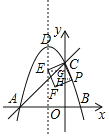
∠ECG+∠PCG＝90°，∠CEG+∠ECG＝90°，∴∠CEG＝∠PGC，

而∠EGC＝∠CPF＝90°，EC＝PC，∴△ECG≌△CPH，

∴EG＝CH＝，则点P坐标为（，）．