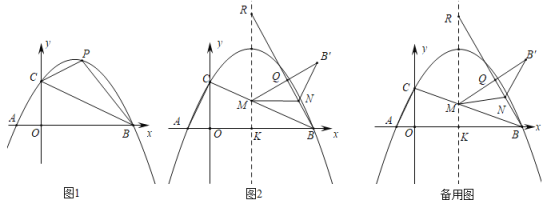
题目内容
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,分别以
,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴和
轴和![]() 轴建立如图所示的平面直角坐标系,
轴建立如图所示的平面直角坐标系,![]() 是
是![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() 重合),过
重合),过![]() 点的反比例函数
点的反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
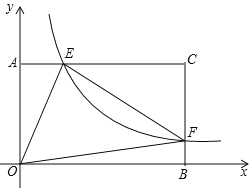
(1)若![]() ,求
,求![]() 点的坐标;
点的坐标;
(2)当点![]() 在
在![]() 上移动时,
上移动时,![]() 与
与![]() 的面积差记为
的面积差记为![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
(3)是否存在这样的点![]() ,使得
,使得![]() 为直角三角形?若存在,求出此时点
为直角三角形?若存在,求出此时点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,S最大值
有最大值,S最大值![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由OA与OB的长,根据C位于第一象限点,即可确定出C的坐标,再求出BF的长即可解决问题;
(2)应分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,利用二次函数求出最值即可.
(3)存在这样的点F,使得△OEF为直角三角形,理由为:由∠EOF为锐角,不可能为直角,设BF=a,由OB=6,得到F(6,a),代入反比例解析式得:k=6a;由OA=4,得到4AE=k=6a,即AE=AE=1.5a,EC=AC-AE=6-1.5a,CF=BC-BF=4-a;分两种情况考虑:当∠OEF为直角时,得到三角形AOE与三角形ECF相似,由相似得比例,将各自的值代入列出关于a的方程,求出方程的解得到a的值;当∠OFE为直角时,同理求出a的值,经检验不合题意,综上得到满足题意a的值.
解:(1)![]() ,
,![]() ,且
,且![]() 在第一象限,
在第一象限,
![]() 的坐标为
的坐标为![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
故答案为:![]() ;
;
(2)解:![]() ,
,![]() 两点坐标分别为
两点坐标分别为![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,
时,![]() 有最大值.
有最大值.
![]() .
.
(3)存在,理由为:
设![]() ,由
,由![]() ,得到
,得到![]() ,代入反比例函数解析式得:
,代入反比例函数解析式得:![]() ;
;
由![]() ,得到
,得到![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
由![]() 为锐角,不可能为直角,
为锐角,不可能为直角,
故分两种情况讨论:
①当![]() 时,可得
时,可得![]() ,
,
又![]() ,且
,且![]() ,
,
![]() ,
,
![]()
![]() ,即
,即![]() ,
,
整理得![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ;
;
②当![]() 时,同理:
时,同理:![]() ,
,
![]()
![]() ,即
,即![]() ,
,
整理得![]() ,
,
解得![]() ,
,![]() 均不合题意,
均不合题意,
![]() ,
,
综上所述,当![]() 时,
时,![]() 为直角三角形.
为直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目