Question

【题目】直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！

（问题探究）

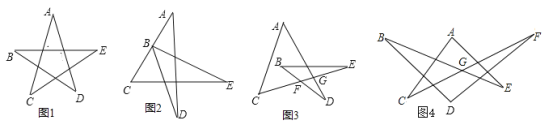
（1）如图1，请直接写出∠A+∠B+∠C+∠D+∠E= ；

（2）将图1变形为图2，∠A+∠DBE+∠C+∠D+∠E的结果如何？请写出证明过程；

（3）将图1变形为图3，则∠A+∠B+∠C+∠D+∠E的结果如何？请写出证明过程．

（变式拓展）

（4）将图3变形为图4，已知∠BGF=160°，那么∠A+∠B+∠C+∠D+∠E+∠F的度数是 ．

Answer 1

【答案】（1）；（2）；证明见解析；（3）；证明见解析；（4）．

【解析】

（1）根据三角形外角的性质∠2=∠C+∠E，∠1=∠A+∠2，根据三角形内角和等于180°即可求解．

（2）根据三角形外角的性质∠ABE=∠C+∠E，∠DBC=∠A+∠D，即可证明此结论．

（3）根据三角形外角的性质，∠DFG=∠B+∠E，∠FGD=∠A+∠C，即可证明此结论．

（4）根据三角形内角和定理和三角形的性质进行转换即可得出答案．

（1）如图1，

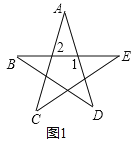
∵∠2=∠C+∠E，∠1=∠A+∠2，

∴∠A+∠B+∠C+∠D+∠E=∠1+∠B+∠D=180°；

故答案为：180°；

（2）将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°．

证明：如图2，

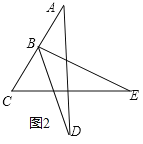
∵∠ABE=∠C+∠E，∠DBC=∠A+∠D，

∠ABE+∠DBE+∠DBC=180°，

∴∠A+∠DBE+∠C+∠D+∠E=180°

∴将图①变形成图②∠A+∠DBE+∠C+∠D+∠E仍然为180°；

（3）将图①变形成图③，则∠A+∠B+∠C+∠D+∠E还为180°．

证明：如图3，

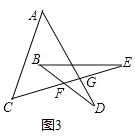
∵在△FGD中，∠DFG+∠FGD+∠D=180°，

∠DFG=∠B+∠E，∠FGD=∠A+∠C，

∴∠A+∠B+∠C+∠D+∠E=180°，

∴将图①变形成图③，则∠A+∠B+∠C+∠D+∠E还为180°．

（4）320°．

如图4，

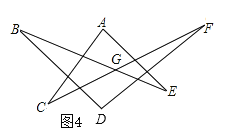
根据三角形中，一个内角的补角等于其余两个内角的和，

∴四边形FGBD中：∠FGB=∠B+∠D+∠F，

四边形ACGE中：∠CGE=∠A+∠C+∠E，

∵∠CGE=∠BGF=160°，

∴∠A+∠B+∠C+∠D+∠E+∠F=320°，

故答案为：320°．