题目内容
【题目】阅读理解:对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在![]() ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
根据上述内容,填空:若m>0,只有当m= 时,![]() 有最小值,最小值为 .
有最小值,最小值为 .
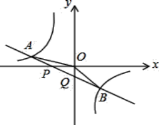
探索应用:如图,已知![]() ,
,![]() ,
,![]() 为双曲线
为双曲线![]() (x>0)上的任意一点,过点
(x>0)上的任意一点,过点![]() 作
作![]() ⊥x轴于点
⊥x轴于点![]() ,
,![]() ⊥y轴于点D.求四边形
⊥y轴于点D.求四边形![]() 面积的最小值,并说明此时四边形
面积的最小值,并说明此时四边形![]() 的形状.
的形状.

【答案】2,2,四边形![]() 面积的最小值为12,四边形ABCD是菱形.
面积的最小值为12,四边形ABCD是菱形.
【解析】
应用上述结论,直接代入即可求出![]() 的最小值;首先设P的坐标为:(x,
的最小值;首先设P的坐标为:(x,![]() ),由S四边形ABCD=S△ABD+S△CBD,可得S四边形ABCD=
),由S四边形ABCD=S△ABD+S△CBD,可得S四边形ABCD=![]() (x+
(x+![]() +4),继而求得答案.
+4),继而求得答案.
解:∵a+b≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() .
.
∴![]() ≥
≥![]() ,
,
∴![]() ≥2,
≥2,
当m=![]() 时,
时,
解得:m=2或-2(不合题意舍去),
故当m=2,最小值是2;
设P的坐标为:(x,![]() ),
),
∵A(-2,0),B(0,-3),
则BD=3+![]() ,OA=2,OC=x,
,OA=2,OC=x,
则S四边形ABCD=S△ABD+S△CBD=![]() 2(3+
2(3+![]() )+
)+![]() x(3+
x(3+![]() )=
)=![]()
![]() =
=![]() (x+
(x+![]() +4)≥
+4)≥![]() ×(2
×(2![]() +4)=12,
+4)=12,
∴当且仅当x=![]() ,即x=2时,四边形ABCD面积有最小值,最小值是12;
,即x=2时,四边形ABCD面积有最小值,最小值是12;
∴点P的坐标为:(2,3),
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.

练习册系列答案
相关题目