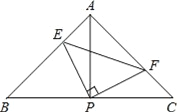
题目内容
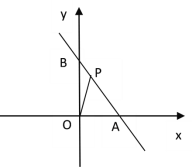
【题目】如图,已知![]() ∥
∥![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,交射线
,交射线![]() 于点
于点![]() ,
,![]() .
.
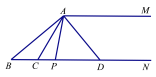
(1)求![]() 的度数;
的度数;
(2)当点![]() 运动时,
运动时,![]() 与
与![]() 之间存在怎样的数量关系?说明理由;
之间存在怎样的数量关系?说明理由;
(3)当点![]() 运动到使
运动到使![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)70°;(2)2:1;(3)35°.
【解析】
(1)根据平行线的性质以及角平分线的定义,即可得到∠CAD的度数;
(2)根据平行线的性质以及角平分线的定义,即可得到∠APB:∠ADB=2:1;
(3)根据平行线的性质以及角平分线的定义,即可得到∠BAC=∠CAP=∠DAP=∠DAM,进而得出∠BAC=![]() ∠BAM=35°.
∠BAM=35°.
(1)∵AM∥BN,
∴∠MAB=180°-∠A=140°,
又∵AC,AD分别平分∠BAP和∠MAP,
∴∠CAD=∠CAP+∠DAP=![]() (∠BAP+∠MAP)=
(∠BAP+∠MAP)=![]() ∠BAM=70°.
∠BAM=70°.
(2)∠APB:∠ADB=2:1.
理由如下:∵AM∥BN,
∴∠APB=∠PAM,∠ADB=∠DAM,
又∵AD平分∠PAM,
∴∠ADB=∠DAM=![]() ∠PAM=
∠PAM=![]() ∠APB,
∠APB,
即∠APB:∠ADB=2:1.
(3)∵AM∥BN,
∴∠ACB=∠CAM,
又∵∠ACB=∠BAD,
∴∠CAM=∠BAD,
∴∠BAC=∠DAM,
又∵∠BAC=∠PAC,∠DAM=∠DAP,
∴∠BAC=∠CAP=∠DAP=∠DAM,
∴∠BAC=![]() ∠BAM=35°.
∠BAM=35°.

【题目】某农产品店利用网络将优质土特产销往全国,其中销售的核桃和花生这两种商品的相关信息如下表:
商品 | 核桃 | 花生 |
规格 | 1 kg/袋 | 2 kg/袋 |
利润 | 10元/袋 | 8元/袋 |
根据上表提供的信息,解答下列问题:
(1)已知今年上半年,该店销售上表规格的核桃和花生共3000kg,获得利润21000元,求上半年该店销售这种规格的核桃和花生各多少袋;
(2)根据之前的销售情况,估计今年下半年,该店还能销售上表规格的核桃和花生共2000kg,其中,核桃的销售量不低于600kg.假设今年下半年,销售上表规格的核桃为![]() (kg),销售上表规格的核桃和花生获得的总利润为
(kg),销售上表规格的核桃和花生获得的总利润为![]() (元),写出
(元),写出![]() 与
与![]() 之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.
之间的函数关系式,并求下半年该店销售这种规格的核桃和花生至少获得的总利润.