Question

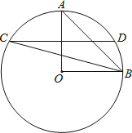
【题目】如图，OA．OB是⊙O的半径且OA⊥OB，作OA的垂直平分线交⊙O于点C．D，连接CB．AB．

求证：∠ABC=2∠CBO．

Answer 1

【答案】证明见解析．

【解析】

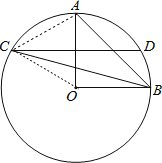
试题分析：连接OC．AC，如图，根据线段垂直平分线的性质得OC=AC，则可判断△OAC是等边三角形，所以∠AOC=60°，于是根据圆周角定理得到∠ABC=∠AOC=30°，然后在△BOC中，由于∠BOC=∠AOC+∠AOB=150°，根据三角形内角和可计算出∠CBO=15°，所以∠ABC=2∠CBO．

试题解析：连接OC．AC，如图，

∵CD垂直平分OA，

∴OC=AC．

∴OC=AC=OA，

∴△OAC是等边三角形，

∴∠AOC=60°，

∴∠ABC=∠AOC=30°，

在△BOC中，∠BOC=∠AOC+∠AOB=150°，

∵OB=OC，

∴∠CBO=15°，

∴∠ABC=2∠CBO．