题目内容
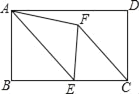
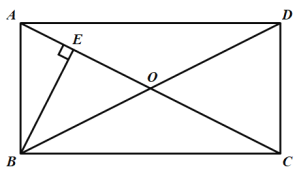
【题目】如图,在![]() ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
(1)求证:![]() ABCD是矩形;
ABCD是矩形;
(2)若AD=![]() ,cos∠ABE=
,cos∠ABE=![]() ,求AC的长.
,求AC的长.
【答案】(1)见解析;(2)5.
【解析】
(1)先说明.OA=OC,OB=OD,再证得AC=BD,即可证明![]() ABCD是矩形;
ABCD是矩形;
(2)先说明∠BAD=∠ADC=90°,再求得∠CAD=∠ABE,最后解直角三角形即可.
(1)证明:∵四边形ABCD是平行四边形
∴OA=OC,OB=OD
又∵OA=OB,
∴OA=OB=OC=OD,
∴AC=BD,
∴![]() OABCD是矩形;
OABCD是矩形;
(2)解∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,
∴∠BAC+∠CAD=90°,
∵BE⊥AC,
∴∠BAC+∠ABE=90°,
∴∠CAD=∠ABE,
在Rt△ACD中,AD=![]() ,cos∠CAD=
,cos∠CAD=![]() =cos∠ABE=
=cos∠ABE=![]()
∴AC=5.

练习册系列答案
相关题目
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.