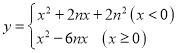��Ŀ����
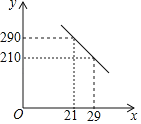
����Ŀ��һ����ѧ��ҵ����Ӧ������������ҵ���ĺ��٣��ڳɶ��и�����������һ���ŵ꣬Ƹ��������Ա�����ƻ�����һ�ֲ�Ʒ����֪�ò�Ʒ�ɱ�����20Ԫ/���������ۼ۲����ڳɱ��ۣ��Ҳ�����30Ԫ/����Ա��ÿ��ÿ��Ĺ���Ϊ200Ԫ�������г����鷢�֣��ò�Ʒÿ���������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵ��ͼ��ʾ��
��1����y��x֮��ĺ�����ϵʽ��
��2����ÿ����Ʒ���ۼ�Ϊ����Ԫʱ��ÿ���ŵ�Ĵ����������������Ƕ��٣����������������멁��Ʒ�ɱ���Ա�����ʣ�
���𰸡���1��y����10x+500��20��x��30������2����x��30ʱ��ÿ���ŵ�Ĵ�����W������Ϊ1600Ԫ��
��������
��1�����ô���ϵ�������y��x֮��ĺ�����ϵʽ��
��2�����ݴ������������멁��Ʒ�ɱ���Ա�������г����κ�������ʽ�����ݶ��κ��������ʽ�ɣ�
�⣺��1����y��x֮��ĺ�����ϵʽΪy��kx+b��
�ѣ�21��290������29��210�����룬
��![]() ��
��
��ã�![]() ��
��
��y��x֮��ĺ�����ϵʽΪy����10x+500��20��x��30����
��2��ÿ���ŵ�Ĵ�����W������10x+500����x��20����400
����10x2+700x��10400
����10��x��35��2+1850��
��20��x��30��
�൱x��30ʱ��ÿ���ŵ�Ĵ�����W������Ϊ1600Ԫ��

 ����5��2���ϵ�д�
����5��2���ϵ�д�