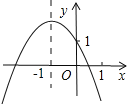Question

【题目】如图，点A（0，2）在y轴上，点B在x轴上，作∠BAC＝90°，并使AB＝AC．

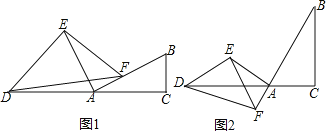
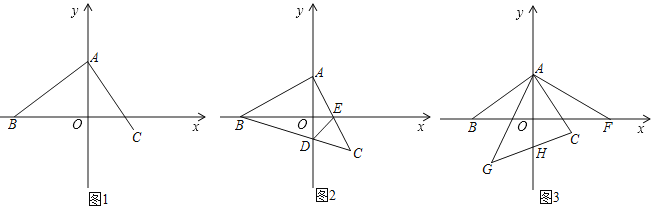
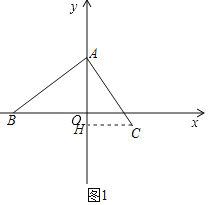
（1）如图1，若点B的坐标为（﹣3，0），求点C的坐标．

（2）如图2，若点B的坐标为（﹣4，0），连接BC交y轴于点D，AC交x轴于点E，连接DE，求证：BE＝AD+DE．

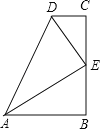
（3）在（1）的条件下，如图3，F为（4，0），作∠FAG＝90°，并使AF＝AG，连接GC交y轴于点H，求点H的坐标．

Answer 1

【答案】（1）C（2，﹣1）；（2）证明见解析；（3）H（0，﹣）．

【解析】

（1）作CH⊥y轴于H，证明△BAO≌△ACH，根据全等三角形的性质求出OH，CH，得到点C的坐标；

（2）作CG⊥AC交y轴于G，分别证明△BAE≌△ACG、△CDG≌△CDE，根据全等三角形的性质得到DG＝DE，结合图形证明；

（3）作GM⊥y轴于M，CN⊥y轴于N，根据（1）的结论求出点G的坐标和点C的坐标，利用待定系数法求出直线CG的解析式，求出点H的坐标．

（1）作CH⊥y轴于H，

则∠HAC+∠C＝90°，

∵∠BAC＝90°，

∴∠HAC+∠BAO＝90°，

∴∠BAO＝∠C，

在△BAO和△ACH中，

，

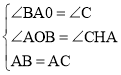∴△BAO≌△ACH（AAS），

∴CH＝OA＝2，AH＝OB＝3，

∴OH＝AH﹣OA＝1，

则点C的坐标为（2，﹣1）；

（2）作CH⊥y轴于H，CG⊥AC交y轴于G，

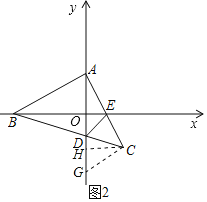
由（1）得，OH＝OA，

∵OE∥CH，

∴AE＝EC，

∵∠AOE＝90°，∠ACG＝90°，

∴∠AEB＝∠CGA，

在△BAE和△ACG中，

，

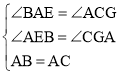∴△BAE≌△ACG（AAS），

∴AG＝BE，CG＝AE＝EC，

在△CDG和△CDE中，

，

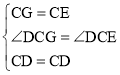∴△CDG≌△CDE（SAS），

∴DE＝DG，

∴BE＝AG＝AD+DG＝AD+DE；

（3）作GM⊥y轴于M，CN⊥y轴于N，

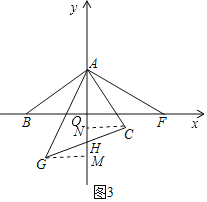
由（1）得，△AOB≌△CNA，△AOF≌△GMA，

∴CN＝OA＝2，GM＝OA＝2，AM＝OF＝4，AN＝OB＝3，

∴ON＝AN﹣OA＝1，OM＝AM﹣OA＝2，

则点G的坐标为（﹣2，﹣2），点C的坐标为（2，﹣1），

设直线CG的解析式为y＝kx+b，

则，

解得，k＝，b＝﹣，

∴直线CG的解析式为y＝x﹣，

当x＝0时，y＝﹣，

∴点H的坐标为（0，﹣）．