题目内容
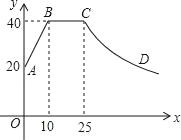
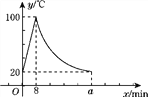
【题目】教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10 ℃，待加热到100 ℃，饮水机自动停止加热，水温开始下降，水温y(℃)和通电时间x(min)成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20 ℃，接通电源后，水温y(℃)和通电时间x(min)之间的关系如图所示，回答下列问题：
(1)分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式；
(2)求出图中a的值；
(3)李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40 ℃的开水，则他需要在什么时间段内接水？
【答案】（1）当0≤x≤8时，y＝10x＋20；当8＜x≤a时，y＝
；（2）a＝40；（3）要想喝到不低于40℃的开水，x需满足8≤x≤20，即李老师要在7：38到7：50之间接水．
【解析】试题分析：（1）当0≤x≤8时，设y＝k1x＋b，将(0，20)，(8，100)的坐标分别代入y＝k1x＋b，即可求得k1、b的值，从而得一次函数的解析式；当8＜x≤a时，设y＝
，将(8，100)的坐标代入y＝
，求得k2的值，即可得反比例函数的解析式；（2）把y＝20代入反比例函数的解析式，即可求得a值；（3）把y＝40代入反比例函数的解析式，求得对应x的值，根据想喝到不低于40 ℃的开水，结合函数图象求得x的取值范围，从而求得李老师接水的时间范围.
试题解析：
(1)当0≤x≤8时，设y＝k1x＋b，
将(0，20)，(8，100)的坐标分别代入y＝k1x＋b，可求得k1＝10，b＝20.
∴当0≤x≤8时，y＝10x＋20.
当8＜x≤a时，设y＝
，
将(8，100)的坐标代入y＝
，
得k2＝800.
∴当8<x≤a时，y＝
.
综上，当0≤x≤8时，y＝10x＋20；
当8＜x≤a时，y＝
.
(2)将y＝20代入y＝
，
解得x＝40，即a＝40.
(3)当y＝40时，x＝
＝20.
∴要想喝到不低于40 ℃的开水，x需满足8≤x≤20，即李老师要在7：38到7：50之间接水．
