题目内容
【题目】已知二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a+b+c<0;②b2-4ac>0;③b>0;④4a-2b+c<0;⑤c-a>1,其中正确的结论有( )
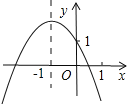
A. ①②④ B. ①②③ C. ①②⑤ D. ①②④⑤
【答案】C
【解析】
根据当x等于1和-2时y的值,可判断①④;再根据开口方向与x轴的交点个数、对称轴、与y轴交点位置判断②③⑤.
由图象知:当x=1时,y=a+b+c<0,①正确;
由图象可以看出抛物线与x轴有两个交点,可得b2-4ac>0,②正确;
∵图象开口向上,对称轴是直线x=-1,
∴a<0,![]() <0,
<0,
∴b<0,③错误;
当x=-2时,y=4a-2b+c=1>0,④错误;
由图象知a<0,c=1,所以c-a>1,⑤正确;
综上,正确的结论为①②⑤.
故选C.

【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小亮做摸球试验,他将盒子内的球搅匀后从中随机摸出一个球,记下颜色后放回,不断重复上述过程,对试验结果进行统计后,小玲得到下表中的数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 1500 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.70 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
则下列结论中正确的是( )
A. n越大,摸到白球的概率越接近0.7
B. 当n=2000时,摸到白球的次数m=1200
C. 当n很大时,摸到白球的频率将会稳定在0.6附近
D. 这个盒子中约有28个白球