Question

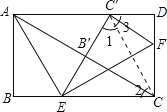
【题目】如图，在矩形ABCD中，AB=4，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在直线EB′与AD的交点C′处，DF=_______．

Answer 1

【答案】

【解析】

连接CC'，可以得到CC'是∠EC'D的平分线，所以CB'=CD，又AB'=AB，所以B'是对角线中点，AC=2AB，所以∠ACB=30°，即可得出答案．

连接CC'．

∵将△ABE沿AE折叠，使点B落在AC上的点B'处，

又将△CEF沿EF折叠，使点C落在EB'与AD的交点C'处，

∴EC=EC'，

∴∠1=∠ECC'．

∵AD∥BC，

∴∠DC'C=∠ECC'，

∴∠1=∠DC'C．

在△CC'B'与△CC'D中，

∵，

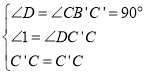∴△CC'B'≌△CC'D，

∴CB'=CD，∠ACC'=∠DCC'．

又∵AB'=AB，

∴AB'=CB'，

∴B'是对角线AC中点，

即AC=2AB=8，

∴∠ACB=30°，

∴∠BAC=60°，∠ACC'=∠DCC'=30°，

∴∠DC'C=∠1=60°，

∴∠DC'F=∠FC'C=30°，

∴C'F=CF=2DF．

∵DF+CF=CD=AB=4，

∴DF．

故答案为：．