题目内容
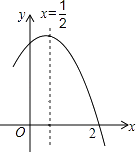
【题目】如图,已知二次函数y=a(x﹣h)2+ ![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0). 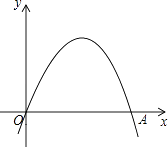
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?
【答案】
(1)解:∵二次函数y=a(x﹣h)2+ ![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
解得:h=1,a=﹣ ![]() ,
,
∴抛物线的对称轴为直线x=1
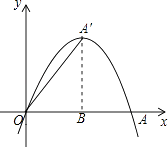
(2)解:点A′是该函数图象的顶点.理由如下:
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,∠OA′B=30°,
∴OB= ![]() OA′=1,
OA′=1,
∴A′B= ![]() OB=
OB= ![]() ,
,
∴A′点的坐标为(1, ![]() ),
),
∴点A′为抛物线y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() 的顶点.
的顶点.
【解析】(1)由于抛物线过点O(0,0),A(2,0),根据抛物线的对称性得到抛物线的对称轴为直线x=1;(2)作A′B⊥x轴于B,先根据旋转的性质得OA′=OA=2,∠A′OA=60°,再根据含30度的直角三角形三边的关系得OB= ![]() OA′=1,A′B=
OA′=1,A′B= ![]() OB=
OB= ![]() ,则A′点的坐标为(1,
,则A′点的坐标为(1, ![]() ),根据抛物线的顶点式可判断点A′为抛物线y=﹣
),根据抛物线的顶点式可判断点A′为抛物线y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() 的顶点.
的顶点.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目