题目内容
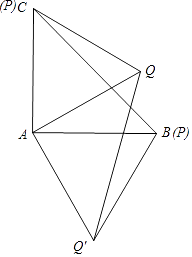
【题目】在△ABC中，∠BAC=90°，AB=AC=2cm，线段BC上一动点P从C点开始运动，到B点停止，以AP为边在AC的右侧作等边△APQ，则Q点运动的路径为cm． 
【答案】2 
【解析】解：如图，Q点运动的路径为QQ′的长， ∵△ACQ和△ABQ′是等边三角形，
∴∠CAQ=∠BAQ′=60°，AQ=AC=AQ′=2cm，
∵∠BAC=90°，
∴∠QAQ′=90°，
由勾股定理得：QQ′= 
= 
=2 ，
∴Q点运动的路径为2 cm；
所以答案是：2 ．
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识，掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°，以及对等边三角形的性质的理解，了解等边三角形的三个角都相等并且每个角都是60°．
练习册系列答案
字词句段篇系列答案
相关题目
