题目内容
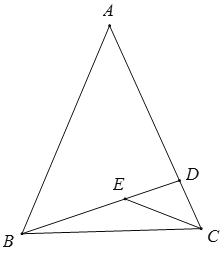
【题目】在平行四边形ABCD中,点E在AD边上,连接BE、CE,EB平分∠AEC
(1)如图1,判断△BCE的形状,并说明理由; 
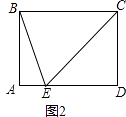
(2)如图2,若∠A=90°,BC=5,AE=1,求线段BE的长. 
【答案】
(1)解:如图1中,结论:△BCE是等腰三角形.
证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴∠CBE=∠AEB,
∵BE平分∠AEC,
∴∠AEB=∠BEC,
∴∠CBE=∠BEC,
∴CB=CE,
∴△CBE是等腰三角形.

(2)解:如图2中,∵四边形ABCD是平行四边形,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠D=90°,BC=AD=5,
在RT△ECD中,∵∠D=90°,ED=AD﹣AE=4,EC=BC=5,
∴AB=CD= ![]() =
= ![]() =3,
=3,
在RT△AEB中,∵∠A=90°AB=3.AE=1,
∴BE= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)结论:△BCE是等腰三角形,根据平行四边形的性质以及已知条件,只要证明∠CBE=∠BEC即可.(2)先证明四边形ABCD是矩形,然后分别在RT△ECD,和RT△ABE中利用勾股定理即可解决问题.
【考点精析】根据题目的已知条件,利用平行四边形的性质的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

练习册系列答案
相关题目