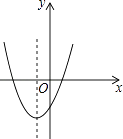题目内容
【题目】如图,直线y=kx﹣2(k>0)与双曲线 ![]() 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 . 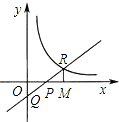
【答案】2 ![]()
【解析】解:∵y=kx﹣2,
∴当x=0时,y=﹣2,
当y=0时,kx﹣2=0,解得x= ![]() ,
,
所以点P( ![]() ,0),点Q(0,﹣2),
,0),点Q(0,﹣2),
所以OP= ![]() ,OQ=2,
,OQ=2,
∵RM⊥x轴,
∴△OPQ∽△MPR,
∵△OPQ与△PRM的面积相等,
∴△OPQ与△PRM的相似比为1,即△OPQ≌△MPR,
∴OM=2OP= ![]() ,RM=OQ=2,
,RM=OQ=2,
所以点R( ![]() ,2),
,2),
∵双曲线 ![]() 经过点R,
经过点R,
∴ ![]() =2,即k2=8,
=2,即k2=8,
解得k1=2 ![]() ,k2=﹣2
,k2=﹣2 ![]() (舍去).
(舍去).
所以答案是:2 ![]() .
.
【考点精析】根据题目的已知条件,利用反比例函数的性质和相似三角形的性质的相关知识可以得到问题的答案,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大;对应角相等,对应边成比例的两个三角形叫做相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目