题目内容
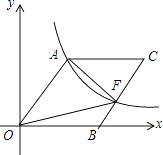
【题目】如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．
（1）填空：点A坐标为；抛物线的解析式为 ．
（2）在图①中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
（3）在图②中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？
【答案】
（1）（1，4）；y=﹣（x﹣1）2+4
（2）
解：依题意有：OC=3，OE=4，
∴CE= 
= 
=5，
当∠QPC=90°时，
∵cos∠QCP= 
= 
，
∴ 
= 
，
解得t= 
；
当∠PQC=90°时，
∵cos∠QCP= 
= ，
∴ 
= ，
解得t= 
．
∴当t= 或t= 时，△PCQ为直角三角形；
（3）
解：∵A（1，4），C（3，0），
设直线AC的解析式为y=kx+b，则 
，解得 
．
故直线AC的解析式为y=﹣2x+6．
∵P（1，4﹣t），将y=4﹣t代入y=﹣2x+6中，得x=1+ 
，
∴Q点的横坐标为1+ ，
将x=1+ 代入y=﹣（x﹣1）2+4中，得y=4﹣ 
．
∴Q点的纵坐标为4﹣ ，
∴QF=（4﹣ ）﹣（4﹣t）=t﹣ ，
∴S△ACQ=S△AFQ+S△CFQ
= 
FQAG+ 
FQDG
= FQ（AG+DG）
= FQAD
= ×2（t﹣ ）
=﹣ +t
=﹣ 
（t2+4﹣4t﹣4）
=﹣ （t﹣2）2+1，
∴当t=2时，△ACQ的面积最大，最大值是1．
【解析】解：（1）∵抛物线的对称轴为x=1，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4），点A在DE上，
∴点A坐标为（1，4），
设抛物线的解析式为y=a（x﹣1）2+4，
把C（3，0）代入抛物线的解析式，可得a（3﹣1）2+4=0，
解得a=﹣1．
故抛物线的解析式为y=﹣（x﹣1）2+4，即y=﹣x2+2x+3；
（1）根据抛物线的对称轴与矩形的性质可得点A坐标，根据待定系数法可得抛物线的解析式；（2）先根据勾股定理可得CE，再分两种情况：当∠QPC=90°时；当∠PQC=90°时；讨论可得△PCQ为直角三角形时t的值；（3）根据待定系数法可得直线AC的解析式，根据S△ACQ=S△AFQ+S△CPQ可得S△ACQ=﹣ （t﹣2）2+1，依此即可求解．
