Question

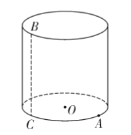
【题目】如图，在一圆柱铁桶内底面的点处有一飞虫，在其上边沿的点处有一面包残渣，已知是点正下方的桶内底面上一点，已知劣弧的长为，铁桶的底面直径为，桶高为60cm，则该飞虫从点到达的最短路径是____________cm．

Answer 1

【答案】

【解析】

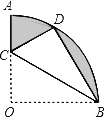
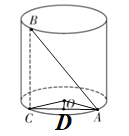
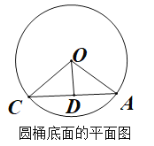
连接AC、AB、OA、OC，作OD⊥AC于点D，先由弧长公式求出∠AOC的度数，然后得到∠AOD的度数，然后利用勾股定理求出AD，然后得到AC，再利用勾股定理求出AB即可.

解：根据题意，连接AC、AB、OA、OC，作OD⊥AC于点D，如图：

∵劣弧的长为，，

∴，

解得：，

即∠AOC=120°，

∵OD⊥AC，

∴∠AOD=∠AOC=60°，

∴∠OAD=30°，

∴OD=OA=10，

∴，

∴，

在Rt△ABC中，，由勾股定理得：

；

∴该飞虫从点到达的最短路径是cm；

故答案为：.