题目内容
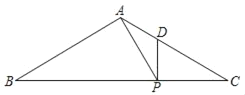
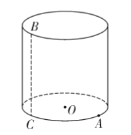
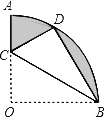
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,求图中阴影部分的面积.
【答案】![]()
【解析】
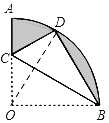
根据题意连接OD,由折叠的性质,可得CD=CO,BD=BO,∠DBC=∠OBC,则可得△OBD是等边三角形,继而求得OC的长,即可求得△OBC与△BCD的面积,又在扇形OAB中,∠AOB=90°,半径OA=2,即可求得扇形OAB的面积,继而求得阴影部分面积.
解:连接OD.
根据折叠的性质,CD=CO,BD=BO,∠DBC=∠OBC,
∴OB=OD=BD,
即△OBD是等边三角形
∴∠DBO=60°,
∴∠CBO=![]() ∠DBO=30°,
∠DBO=30°,
∵∠AOB=90°,
∴OC=OBtan∠CBO=2×![]() ,
,
∴S△BDC=S△OBC=![]() ×OB×OC=
×OB×OC=![]() ×2×
×2×![]() ,
,
S扇形AOB=![]() =π,
=π,
∴阴影部分的面积为:S扇形AOB﹣S△BDC﹣S△OBC=π﹣![]() =
=![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.