题目内容
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.
(1)求证:CF是⊙O的切线;
(2)当BD=![]() ,sinF=
,sinF=![]() 时,求OF的长.
时,求OF的长.
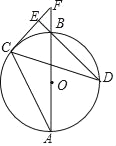
【答案】(1)见解析;(2)OF=5.
【解析】
(1)连接OC.先根据等边对等角及三角形外角的性质得出∠3=2∠1,由已知∠4=2∠1,得到∠4=∠3,则OC∥DB,再由CE⊥DB,得到OC⊥CF,根据切线的判定即可证明CF为⊙O的切线;
(2)连接AD.由圆周角定理得出∠D=90°,证出∠BAD=∠F,得出sin∠BAD=sin∠F=![]() ,求出AB=
,求出AB=![]() BD=6,得出OB=OC=3,再由sinF=
BD=6,得出OB=OC=3,再由sinF=![]() 即可求出OF.
即可求出OF.
(1)连接OC.如图1所示:
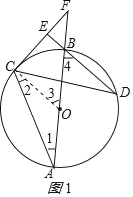
∵OA=OC,
∴∠1=∠2.
又∵∠3=∠1+∠2,
∴∠3=2∠1.
又∵∠4=2∠1,
∴∠4=∠3,
∴OC∥DB.
∵CE⊥DB,
∴OC⊥CF.
又∵OC为⊙O的半径,
∴CF为⊙O的切线;
(2)连接AD.如图2所示:

∵AB是直径,
∴∠D=90°,
∴CF∥AD,
∴∠BAD=∠F,
∴sin∠BAD=sinF=![]() ,
,
∴AB=![]() BD=6,
BD=6,
∴OB=OC=3,
∵OC⊥CF,
∴∠OCF=90°,
∴sinF=![]() ,
,
解得:OF=5.

【题目】今年我国多个省市遭受严重干旱,受旱灾的影响,4月份,我市某蔬菜价格呈上升趋势,其前四周每周的平均销售价格变化如表:
周数x | 1 | 2 | 3 | 4 |
价格y(元/千克) | 2 | 2.2 | 2.4 | 2.6 |
(1)请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x的函数关系式;
(2)进入5月,由于本地蔬菜的上市,此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克,且y与周数x的变化情况满足二次函数y=﹣![]() x2+bx+c,请求出5月份y与x的函数关系式;
x2+bx+c,请求出5月份y与x的函数关系式;
(3)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=![]() x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=﹣![]() x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?