题目内容
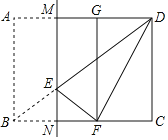
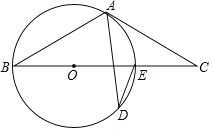
【题目】如图，在四边形ABCD中，AD∥BC，E为BC的中点，BC＝2AD，EA＝ED，AC与ED相交于点F.
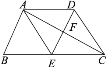
(1)求证：四边形AECD是平行四边形；
(2)试探究AB、CD之间的数量关系，并证明你的结论；
(3)当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由；若EA＝ED＝2，求此时菱形AECD的面积．
【答案】（1）详见解析；（2）详见解析；（3）2
【解析】
根据已知条件，只要证明：AD=EC，AD∥EC即可.
根据已知条件，想办法证明：AB=DE，CD=DE即可.
假定四边形AECD为菱形时，根据菱形对角线知：AC⊥ED，又ED∥AB，故猜想AB⊥AC时，四边形AECD为菱形；求面积时由菱形面积公式：对角线乘积的一半即可求解.
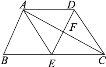
解：(1)∵E是BC的中点，∴BE＝EC＝
BC，
∵BC＝2AD，即AD=
∴AD＝BE=EC，又∵AD∥EC，
∴四边形AECD是平行四边形.
(2)由(1)知：四边形AECD是平行四边形.
∴AE＝CD，
又由已知有：AE＝ED，∴ED＝CD……①
∵AD＝BE，AD∥BE，
∴四边形ABED是平行四边形，
∴AB＝ED……②
结合①②可知
∴AB＝CD.
故AB和CD的数量关系为：AB=CD.
(3)当AB⊥AC时，四边形AECD是菱形.
理由如下：∵四边形ABED是平行四边形，
∴AB∥DE，
∵AB⊥AC，∴ED⊥AC，
∵四边形AECD是平行四边形，
∴四边形AECD是菱形.
∵AE＝DE＝2，
∴EF＝DF＝1，
在Rt△AFE中，AF＝
＝
，AC＝2AF＝
∴
.
故菱形AECD的面积为
练习册系列答案
阅读快车系列答案
相关题目
