Question

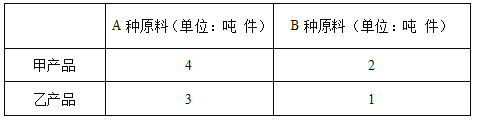
【题目】平某游泳馆暑期推出两种游泳付费方式，方式一：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费20元；方式二：不购买会员证，每次游泳付费25元．设小明计划今年暑期游泳次数为x（x为正整数）．根据题意列表：

游泳次数	5	8	10	…	x
方式一的总费用（元）	200	260	m	…
方式二的总费用（元）	125	200	250	…

（1）表格中的m值为 ；

（2）根据题意分别求出两种付费方式中与自变量x之间的函数关系式并画出图象；

（3）请你根据图象，帮助小明设计一种比较省钱的付费方案．

Answer 1

【答案】（1）m=300；（2）；；(3)当x＝20时，选择两种付费方式一样多；当x＞20时，选择第一种付费方式比较省钱；当x＜20时，选择第二种付费方式比较省钱．

【解析】

（1）根据题意求出m的值即可；

（2）利用待定系数法．将（5，200）（8，260）代入，即可求得方式一的解析式，同理可求得方式二的解析式；

（3）通过观察，进行判断哪种付费方式更合算．

（1）游泳次数是10时，m=100+20×10=300；

（2）（1）设方式一的解析式为：y=kx+b

将（5，200）（8，260）代入得

，解得

故方式一的解析为：y=20x+100

设方式二的解析式为：y1=k1x，

将（5，125）代入得k1=25

故方式二的解析式为：y1=25x；

画出图象如图

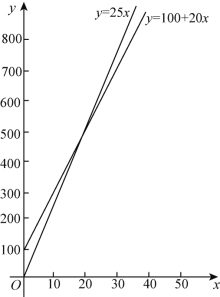
(3)当x＝20时，选择两种付费方式一样多；

当x＞20时，选择第一种付费方式比较省钱；

当x＜20时，选择第二种付费方式比较省钱．