Question

【题目】如图1，一次函数y=x+2的图象交y轴于点A，交x轴于点B，点E在x轴的正半轴上，OE=8，点F在射线BA上，过点F作x轴的垂线，点D为垂足，OD=6．

（1）写出点F的坐标　 　；

（2）求证：∠ABO=45°；

（3）操作：将一块足够大的三角板的直角顶点放在线段BF的中点M处，一直角边过点E，交FD于点C，另一直角边与x轴相交于点N，如图2，求点N的坐标．

Answer 1

【答案】（1）6；（2）证明见解析（3）N（﹣，0）．

【解析】（1）首先求出A、B两点坐标，推出OA=OB=2，再证明△BDF是等腰直角三角形即可解决问题．

（2）根据等腰直角三角形的性质即可证明；

（3）想办法求出直线MN的解析式即可解决问题；

（1）对于一次函数y=x+2，令x=0得到y=2，令y=0，得到x=﹣2，∴A（0，2），B（﹣2，0），∴OB=OA=2，∴∠ABO=∠BAO=45°．

∵OD=6，∴BD=OB+OD=8．

∵FD⊥x轴，∴∠FDB=90°，∴∠DBF=∠DFB=45°，∴DB=DF=8，∴F（6，8）．

（2）在Rt△OAB中，∵OA=OB=2，∴∠ABO=∠OAB=45°．

（3）∵B（﹣2，0），F（6，8），MB=MF，∴M（2，4）．

∵E（8，0），设直线EM的解析式为y=kx+b，则有，解得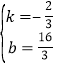：，∴直线EM的解析式为y=﹣x+．

∵MN⊥EM，∴可以假设直线MN的解析式为y=x+b′，把M（2，4）代入得：b′=1

∴直线MN的解析式为y=x+1，∴N（﹣，0）．