题目内容
【题目】如图,在△ABC中,DM、EN分别垂直平分AC和BC,交AB于M、N,
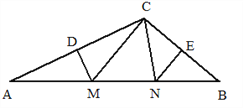
(1)若△CMN的周长为21cm,求AB的长;
(2)若∠MCN=50°,求∠ACB的度数.
【答案】(1)AB=21 (cm);(2)∠ACB=115°
【解析】试题分析:(1)本题利用垂直平分线的性质即可解决,(2)利用等腰三角形的性质和外角性质得出.
试题解析:(1) ∵ DM、EN分别垂直平分AC和BC
∴ AM=MC, CN=NB
∵ △CMN的周长= CM+CN+MN =21
∴ AB=AM+MN+NB=CM+MN+CN=21 (cm)
(2) ∵ ∠MCN=50°
∴ ∠CMN+∠CNM=180°-50°=130°
∵ AM=MC, CN=NE
∴∠A=∠ACM, ∠B=∠BCN
∵ ∠A+∠ACM=∠CMN, ∠B+∠BCN=∠CNM
∴ ∠ACM=![]() ∠CMN, ∠BCN=
∠CMN, ∠BCN=![]() ∠CNM
∠CNM
∴ ∠ACM +∠BCN=![]() ( ∠CMN+∠CNM )=65°
( ∠CMN+∠CNM )=65°
∴ ∠ACB=65°+50°= 115°

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目