题目内容
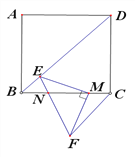
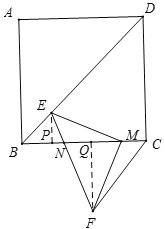
【题目】如图在正方形ABCD中,点M为BC边上一点,BM=4MC,以M为直角顶点作等腰直角三角形MEF,点E在对角线BD上,点F在正方形外EF交BC于点N,连CF,若BE=2,S△CMF=3,则MN=_____.
【答案】![]()
【解析】分别过点E、F作EP⊥BC,FQ⊥BC,垂足分别为P、Q,
∴∠BPE=∠EPM=∠FQM=∠FQN=90°,∴EP//FQ,
∴∠PEM+∠EMP=90°,
∵∠EMP+∠QMF=∠EMF=90°,
∴∠PEM=∠QMF,
又∵ME=MF,∴△PEM≌△QMF,∴PE=MQ,PM=FQ,
∵四边形ABCD是正方形,∴∠DBC=45°,∵∠BPE =90°,∴∠BEP=45°=∠EBP,
∴BP=PE=![]() BE=
BE=![]() ,
,
∴BM=![]() +PM=
+PM=![]() +FQ,
+FQ,
∵BM=4CM,S△CMF=![]() =3,
=3,
∴FQ=3![]() ,
,
∴PQ=PM=MQ=3![]() -
-![]() =2
=2![]() ,
,
∵EP//FQ,∴△EPN∽△FQN,∴EP:FQ=PN:NQ,
即:![]() :3
:3![]() =(2
=(2![]() -NQ):NQ,
-NQ):NQ,
∴NQ=![]() ,
,
∴MN=NQ+MQ=![]() +
+![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目