题目内容
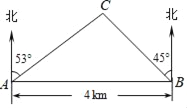
【题目】如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东53°方向上,从B测得灯塔C在北偏西45°方向上,求灯塔C与观测点A的距离(精确到0.1km).(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
【答案】灯塔C与观测点A的距离为2.9km.
【解析】
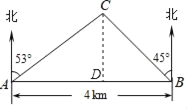
如图,过点C作CD⊥AB,构建直角△ACD和直角△BCD.通过解Rt△ADC得到AD=ACcos37°,CD=ACsin37°,通过解Rt△BDC得到BD=CD.所以由AB=AD+DB来求AC的长度.
解:如图,作CD⊥AB,垂足为D.
由题意可知:∠CAB=90°﹣53°=37°,
∠CBA=90°﹣45°=45°,
∴在Rt△ADC中,
cos∠CAB=![]() ,即AD=ACcos37°;
,即AD=ACcos37°;
sin∠CAB=![]() ,即CD=ACsin37°.
,即CD=ACsin37°.
在Rt△BDC中,tan∠CBA=![]() ,即BD=
,即BD=![]() =CD.
=CD.
∵AB=AD+DB,
∴ACcos37°+ACsin37°=4.
∴AC=![]() ≈2.9km.
≈2.9km.
答:灯塔C与观测点A的距离为2.9km.

练习册系列答案
相关题目