题目内容
【题目】(基础巩固)
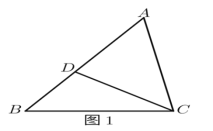
(1)如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证:AC2=ADAB.
(尝试应用)
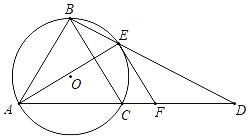
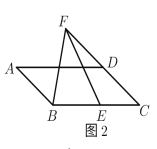
(2)如图2,在ABCD中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
(拓展提高)
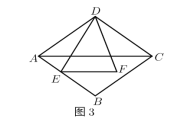
(3)如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF,∠EDF=![]() ∠BAD,AE=2,DF=5,求菱形ABCD的边长.
∠BAD,AE=2,DF=5,求菱形ABCD的边长.
【答案】(1)见解析;(2)AD=![]() ;(3)5
;(3)5![]() ﹣2
﹣2
【解析】
(1)根据题意证明△ADC∽△ACB,即可得到结论;
(2)根据现有条件推出△BFE∽△BCF,再根据相似三角形的性质推断,即可得到答案;
(3)如图,分别延长EF,DC相交于点G,先证明四边形AEGC为平行四边形,再证△EDF∽△EGD,可得![]() ,根据EG=AC=2EF,可得DE=
,根据EG=AC=2EF,可得DE=![]() EF,再根据
EF,再根据![]() ,可推出DG=
,可推出DG=![]() DF=5
DF=5![]() ,即可求出答案.
,即可求出答案.
解:(1)证明:∵∠ACD=∠B,∠A=∠A,
∴△ADC∽△ACB,
∴![]() ,
,
∴AC2=ADAB;
(2)∵四边形ABCD是平行四边形,
∴AD=BC,∠A=∠C,
又∵∠BFE=∠A,
∴∠BFE=∠C,
又∵∠FBE=∠CBF,
∴△BFE∽△BCF,
∴![]() ,
,
∴BF2=BEBC,
∴BC=![]() =
=![]() =
=![]() ,
,
∴AD=![]() ;
;
(3)如图,分别延长EF,DC相交于点G,
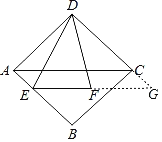
∵四边形ABCD是菱形,
∴AB∥DC,∠BAC=![]() ∠BAD,
∠BAD,
∵AC∥EF,
∴四边形AEGC为平行四边形,
∴AC=EG,CG=AE,∠EAC=∠G,
∵∠EDF=![]() ∠BAD,
∠BAD,
∴∠EDF=∠BAC,
∴∠EDF=∠G,
又∵∠DEF=∠GED,
∴△EDF∽△EGD,
∴![]() ,
,
∴DE2=EFEG,
又∵EG=AC=2EF,
∴DE2=2EF2,
∴DE=![]() EF,
EF,
又∵![]() ,
,
∴DG=![]() DF=5
DF=5![]() ,
,
∴DC=DG﹣CG=5![]() ﹣2.
﹣2.

 阅读快车系列答案
阅读快车系列答案