题目内容
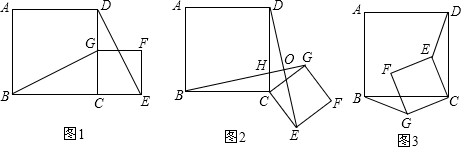
设正方形ABCD的边CD的中点为E，F是CE的中点（图）．求证：∠DAE=
∠BAF．
| 1 |
| 2 |
证明：如图，作∠BAF的平分线AH交DC的延长线于H，则∠1=∠2=∠3，
所以FA=FH．
设正方形边长为a，在Rt△ADF中，
AF2=AD2+DF2=a2+(
)2=
a2，
所以AF=
a=FH．
从而CH=FH-FC=
a-
=a，
所以Rt△ABG≌Rt△HCG（AAS），GB=GC=DE=
a．
从而Rt△ABG≌Rt△ADE（SAS），
所以∠DAE=∠2=
∠BAF．
所以FA=FH．
设正方形边长为a，在Rt△ADF中，
AF2=AD2+DF2=a2+(
| 3a |
| 4 |
| 25 |
| 16 |
所以AF=
| 5 |
| 4 |
从而CH=FH-FC=
| 5 |
| 4 |
| a |
| 4 |
所以Rt△ABG≌Rt△HCG（AAS），GB=GC=DE=
| 1 |
| 2 |
从而Rt△ABG≌Rt△ADE（SAS），
所以∠DAE=∠2=
| 1 |
| 2 |
练习册系列答案
相关题目
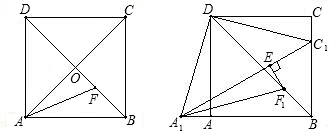
顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），顶点C、D都在第一象限．