题目内容
等腰梯形ABCD中,AD∥BC,AB=DC=12,AD=4,∠B=60°,点P是腰AB上的一个动点.
(1)求BC的长.
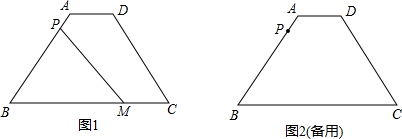
(2)如图1,如果点M在BC上,BM=12,PM平分梯形ABCD的面积,求出此时PB的长;
(3)过点P作直线PM,是否存在PM将梯形ABCD的周长和面积同时平分?若存在,求出此时PB的长;若不存在,请说明理由;
(1)求BC的长.
(2)如图1,如果点M在BC上,BM=12,PM平分梯形ABCD的面积,求出此时PB的长;
(3)过点P作直线PM,是否存在PM将梯形ABCD的周长和面积同时平分?若存在,求出此时PB的长;若不存在,请说明理由;

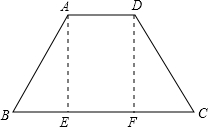
(1)过点A作AE⊥BC,DF⊥BC,
∵∠B=60°,AB=12,
∴sin60°=
| AE |
| 12 |
∴AE=6
| 3 |
∴BE=6,同理可证:FC=6,
∴BC=BE+EF+FC=6+4+6=16;
(2)作△PBM的高PG,
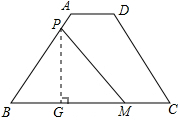
∵等腰梯形ABCD的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵PM平分梯形ABCD的面积,
∴S△PBM=30
| 3 |
∵BM=12,
∴PG=5
| 3 |
∵∠B=60°,
∴PB=
5
| ||
| sin60° |
∴PB=10;
(3)当M在BC上时,梯形ABCD的周长是4+12+16+12=44,
∵PB=10,BM=12时PB+BM=22(符合题意),
PB=12,BM=10时 PB+BM=22(符合题意),
当M在DC上时(舍去),
当M在AD上(舍去),
则存在符合题意的直线PM.

练习册系列答案
相关题目

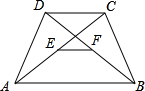 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是