题目内容
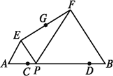
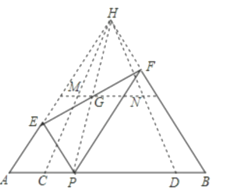
【题目】如图所示,已知AB= 6,点C,D在线段AB上,AC =DB = 1,P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边△AEP和等边△PFB,连接EF,设EF的中点为G,当点P从点C运动到点D时,则点G移动路径的长是_________.
【答案】2
【解析】
分别延长AE,BF交于点H,易证四边形EPFH为平行四边形,得出点G为PH的中点,则G的运动轨迹为△HCD的中位线MN,再求出CD的长度,运用中位线的性质求出MN的长度即可.
解:如图,分别延长AE,BF交于点H,
∵∠A=∠FPB=60°,
∴AH∥PF,
∵∠B=∠EPA=60°,
∴BH∥PE
∴四边形EPFH为平行四边形,
∴EF与HP互相平分,
∵点G为EF的中点,
∴点G为PH的中点,即在P运动的过程中,G始终为PH的中点,
∴G的运动轨迹为△HCD的中位线MN,
∵CD=6-1-1=4,
∴MN=![]() =2,
=2,
∴点G移动路径的长是2,
故答案为:2.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目