Question

【题目】Rt△ABC的边AB=5，AC=4，BC=3，矩形DEFG的四个顶点都在Rt△ABC的边上，当矩形DEFG的面积最大时，其对角线的长为_______．

Answer 1

【答案】或

【解析】

分两种情形画出图形分别求解即可解决问题

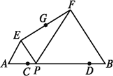
情况1：如图1中，四边形DEFG是△ABC的内接矩形，设DE=CF=x，则BF=3-x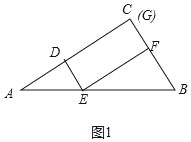

∵EF∥AC，

∴=

∴=

∴EF=(3-x)

∴S矩形DEFG=x(3-x)=﹣(x-)2+3

∴x=时，矩形的面积最大，最大值为3，此时对角线=．

情况2：如图2中，四边形DEFG是△ABC的内接矩形，设DE=GF=x，

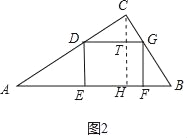
作CH⊥AB于H，交DG于T．则CH=，CT=﹣x，

∵DG∥AB，

∴△CDG∽△CAB，

∴

∴

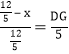
∴DG=5﹣x，

∴S矩形DEFG=x（5﹣x）=﹣（x﹣）2+3，

∴x=时，矩形的面积最大为3，此时对角线==

∴矩形面积的最大值为3，此时对角线的长为或

故答案为或